Bài 1: 

Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:

\(AC^2=BC^2+AB^2\)

\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)

hay \(AB=4\sqrt{5}cm\)

Vậy: \(AB=4\sqrt{5}cm\)

Bài 2: 

Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:

\(MP^2=MN^2+NP^2\)

\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)

hay MN=4cm

Vậy: MN=4cm

Bài 1 :

- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)

\(\Leftrightarrow AB^2+8^2=12^2\)

\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )

Vậy ...

Bài 2 :

- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :

\(MN^2+NP^2=MP^2\)

\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)

\(\Leftrightarrow MN=4\) ( đvđd )

Vậy ...

a: Xét ΔABC vuông tại B và ΔAED vuông tại E có

AC=AD

\(\widehat{A}\) chung

Do đó: ΔABC=ΔAED

b: Đề sai rồi bạn

3:

góc C=90-50=40 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin40

=>\(BC\simeq6,22\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)

1:

góc C=90-60=30 độ

Xét ΔABC vuông tại A có

sin B=AC/BC

=>3/BC=sin60

=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)

=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

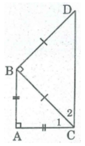
Vì ΔABC vuông cân tại A nên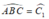 

Lại có: 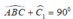 ( tính chất tam giác vuông).

Suy ra: ∠ C 1 = 45 0

Vì ∆ BCD vuông cân tại B nên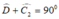 

Lại có:  ( tính chất tam giác vuông).

Suy ra:  ∠ C 2 =  45 0

∠ (ACD) = ∠ C 1 +  ∠ C 2 =  45 0  +  45 0  =  90 0

⇒ AC ⊥ CD

Mà AC ⊥ AB (gt)

Suy ra: AB //CD

Vậy tứ giác ABCD là hình thang vuông.

SBT TRAG BAO NHIÊU Ạ

ΔBDC vuông cân tại B

=>góc BCD=góc BDC=45 độ

ΔABC vuông cân tại A

=>góc ABC=góc ACB=45 độ

góc ABC=góc DCB

mà hai góc này ở vị trí so le trong

nên AB//DC

mà AB vuông góc AC

nên DC vuông góc AC

Xét tứ giác ABDC có

AB//DC
góc CAB=90 độ

Do đó: ABDC là hình thang vuông

Câu 1: B

Câu 2:Sửa đề: \(AD^2=DE^2+AE^2\)

=> Chọn A

Câu 3: Chọn D

Câu 4: \(EF=3\sqrt{2}cm\)

Câu 1 là 70 bạn nhé

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có

BE chung

góc ABE=góc HBE

=>ΔBAE=ΔBHE

b: Xét ΔEBC có góc EBC=góc ECB

nên ΔEBC cân tại E

mà EH là đường cao

nên H là trung điểm của BC

=>HB=HC

d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có

EA=EH

góc AEI=góc HEC

=>ΔEAI=ΔEHC

=>EI=EC>EH

+)ΔABC vuông tại A \(\Rightarrow\widehat{A}=90^o\)

+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(=>90^o+40^o+\widehat{C}=180^o\)

\(=>\widehat{C}=180^o-90^o-40^o=50^o\)

Vậy \(\widehat{C}=50^o\)

------------------------------------------

+)Tam giác ABC vuông tại B \(\Rightarrow\widehat{B}=90^o\)

+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}+\widehat{C}=2.\widehat{C}+\widehat{C}=3.\widehat{C}\)

+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{A}+90^o+\widehat{C}=180^o\)

\(=>\widehat{A}+\widehat{C}=180^o-90^o\)

\(=>3.\widehat{C}=90^o\)

\(=>\widehat{C}=\dfrac{90^o}{3}=30^o\)

+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}=2.30^o=60^o\)

Vậy: \(\widehat{A}=60^o\) ; \(\widehat{C}=30^o\)

1: góc C=90-40=50 độ

2: góc A=2/3*90=60 độ

góc C=90-60=30 độ