3. Cho góc nhọn xOy. Từ điểm I trong góc đó kẻ các tia Im // Ox; In // Oy.
a) Hãy chứng tỏ xOy = mIn.
b) Có nhận xét gì về mối quan hệ giữa các cạnh của 2 góc ấy?
Gíup mình với cảm ơn các bạn nhiều!!!
3. Cho góc nhọn xOy. Từ điểm I trong góc đó kẻ các tia Im // Ox; In // Oy.
a) Hãy chứng tỏ xOy = mIn.
b) Có nhận xét gì về mối quan hệ giữa các cạnh của 2 góc ấy?
Gíup mình với cảm ơn các bạn nhiều!!!
cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
a: Xét ΔOIA và ΔOIB có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOIA=ΔOIB
b: Xét ΔONI vuông tại N và ΔOMI vuông tại M có
OI chung
\(\widehat{NOI}=\widehat{MOI}\)
Do đó: ΔONI=ΔOMI
Suy ra: IN=IM
cho góc nhọn xOy, Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA =OB . Gọi I là giao điểm của Oz và AB.
a) Chứng minh: . tam giác OIA tam giác OIB Chứng minh Oz vuông góc AB .
b) Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox ,M thuộc Oy) . Chứng minh: IM =IN .
c) Chứng minh: góc BIM = góc AIN .
d)Chứng minh: MN // AB
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
a) Xét tam giác \(OIA\) và tam giác \(OIB\) có:
\(OA=OB\)
\(\widehat{AOI}=\widehat{BOI}\)
\(OI\) cạnh chung
suy ra \(\Delta OIA=\Delta OIB\) (c.g.c)
b) Xét tam giác \(OIN\) và tam giác \(OIM\):
\(\widehat{ION}=\widehat{IOM}\)
\(OI\) cạnh chung
\(\widehat{ONI}=\widehat{OMI}\left(=90^o\right)\)
suy ra \(\Delta OIN=\Delta OIM\) (cạnh huyền - góc nhọn)
\(\Rightarrow IN=IM\)
c) \(\Delta OIA=\Delta OIB\) suy ra \(IA=IB\).
Xét tam giác \(INA\) và tam giác \(IMB\):
\(IA=IB\)
\(\widehat{INA}=\widehat{IMB}\left(=90^o\right)\)
\(IN=IM\)
suy ra \(\Delta INA=\Delta IMB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{AIN}=\widehat{BIM}\)
d) \(\Delta OIN=\Delta OIM\) suy ra \(ON=OM\)
suy ra \(\dfrac{ON}{OA}=\dfrac{OM}{OB}\) suy ra \(MN//AB\).
Cho góc nhọn xOy,Oz là tia phân giác của góc đó.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Gọi I là giao điểm của Oz và AB.a) CM:∆OIA=∆OIB.CM:Oz vuông góc với AB.b)Từ I kẻ IN vuông góc Ox và IM vuông góc Oy(N thuộc Ox,M thuộc Oy).CM: IM=IN.c)CM:góc BIM=góc AIN.d)CM:MN song song AB
a) Xét △OIA và △OIB có:
OA = OB
\(\widehat{AOI}=\widehat{BOI}\)
OI : cạnh chung
Suy ra △OIA = △OIB (c.g.c)
Ta lại có △OAB có OA = OB nên △OAB là tam giác cân tại O
Vì Oz là đường phân giác của △OAB nên Oz đồng thời là đường
cao của △OAB.
Suy ra \(Oz\perp AB\)(*)
b)△INO có \(\widehat{OIN}+\widehat{N}+\widehat{ION}\)= 180o (tổng ba góc của một tam giác)
△IMO có \(\widehat{OI}M+\widehat{M}+\widehat{IOM}\)= 180o (tổng ba góc của một tam giác)
Mà \(\widehat{ION}=\widehat{IOM};\widehat{N}=\widehat{M}=90^o\)
Nên \(\widehat{OIN}=\widehat{OIM}\)
Xét △IMO và △INO có :
\(\widehat{OIN}=\widehat{OIM}\)
IO : cạnh chung
\(\widehat{ION}=\widehat{IOM}\)
Suy ra △IMO = △INO (g.c.g) (**)
Nên IM = IN
c) Từ (*) suy ra \(\widehat{BIO}=\widehat{AIO}=90^o\)
Mặc khác \(\widehat{BIO}=\widehat{BIM}+\widehat{MIO}\)
\(\widehat{AIO}=\widehat{AIN}+\widehat{NIO}\)
Mà\(\widehat{MIO}=\widehat{NIO}\)(từ (**) suy ra)
Nên \(\widehat{BIM}=\widehat{AIN}\)
d)Gọi T là giao điểm của MN và tia Oz
Từ (*) suy ra △AIO vuông tại I và △OTN vuông tại T.
nên \(\widehat{AIO}=\widehat{NTO}=90^o\)
△AIO có: \(\widehat{A}+\widehat{AIO}+\widehat{IOA}\) = 180o(tổng ba góc của một tam giác)
△OTN có: \(\widehat{TNO}+\widehat{NTO}+\widehat{TON}\) = 180o(tổng ba góc của một tam giác)
Mà \(\widehat{AIO}=\widehat{NTO}=90^o\)và \(\widehat{IOA}=\widehat{TON}\)
Suy ra \(\widehat{A}=\widehat{TNO}\)
Nên MN//AB
cho góc nhọn xOy . Từ I trong góc xOy kẻ In // Ox và Im // Oy. chứng minh góc xOy=góc nIm
có nx vẽ mối quan hệ giữa 2 cạnh của góc đó
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.
a) Chứng minh tam giác AOC = tam giác BOC.
b) Chứng minh CB I Oy.
c) Chứng minh OC là đường trung trực của đoạn thẳng AB.
d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.
e) Giả sử góc xOy = 60° và OH = 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
b: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB vuông góc Oy
c: OA=OB
CA=CB
=>OC là trung trực của AB
Cho góc nhọn xOy với Ot là tia phân giác. Trên Ot lấy điểm I, từ I kẻ IA ⊥ Ox tại A, tia AI cắt Oy tại N, kẻ IB ⊥ Oy tại B, tia BI cắt Ox tại M. Khi đó ta có:
A. IA = IB
B. OA = OB
C. IM = IN
D. Cả A, B, C đều đúng
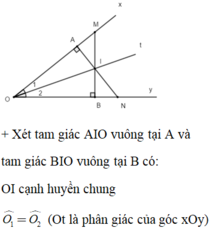
Do đó: Δ A I O = Δ B I O (cạnh huyền – góc nhọn)
Suy ra OA = OB ; IA = IB (hai cạnh tương ứng)
+ Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
IA = IB (cmt)

Cho góc nhọn xOy. Lấy điểm H nằm trong góc xOy. Từ H kẻ HE ⊥ Ox tại E, HF ⊥ Oy tại F. Trên tia HE lấy điểm sao cho E là trung điểm của HM, trên tia HF lấy điểm N sao cho F là trung điểm của HN. Khi đó:
A. OM = OH = ON
B. E O F ^ = 1 2 M O N ^
C. Câu A đúng, câu B đúng
D. Câu A đúng, câu B sai