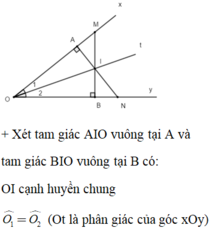
Do đó: Δ A I O = Δ B I O (cạnh huyền – góc nhọn)
Suy ra OA = OB ; IA = IB (hai cạnh tương ứng)
+ Xét tam giác IAM vuông tại A và tam giác IBN vuông tại B có:
IA = IB (cmt)
Cho góc nhọn xOy với Ot là tia phân giác. Trên Ot lấy điểm I, từ I kẻ IA ⊥ Ox tại A, tia AI cắt Oy tại N, kẻ IB ⊥ Oy tại B, tia BI cắt Ox tại M. so sánh hai góc M I t ^ và N I t ^
A. M I t ^ > N I t ^
B. M I t ^ < N I t ^
C. M I t ^ = N I t ^
D. M I t ^ = 2 N I t ^
cho góc nhọn ot là tia phân giác, trên tia ot lấy điểm I.từ I kẻ IA vuông góc Ox ,IB vuông góc OY .đường thẳng Ia cắt ox tại D cm;
a)góc OCI=gócODI
b)ot vuông góc cd
c)ab//cd
Cho góc nhọn xOy có Ot là tia phân giác. Trên Ot lấy điểm I tùy ý, Vẽ IA vuông góc Ox tai A, tia AI cắt Oy tai N. vẽ IB vuông góc với Oy tại B, Tia BI cắt Ox tại M A. OA=OB B. IA = IB C. IN=IM D. A,B,C đều đúng
7 ) Cho Ot là tia phân giác của góc ^ xOy ( xOy là góc nhọn ) . Lấy I bất kỳ thuộc Ot qua I kẻ IA vuông góc Ox tại A và AI cắt Oy tại D . Qua I kẻ IB cắt Ox tại C
a ) cmr Tam giác OIA = Tam giác OIB
b ) cmr Tam giác OIC =Tam giác OID , OC= OD
c )OI vuông góc CD
d ) Cho xOy = 60 độ ; OI = 8 cm . Tính OA
cho góc xoy khác góc bẹt , ot là tia phân giác của góc đó. qua điểm M thuộc tia ot kẻ đường vuông góc với Ox và Oy theo thứ tự tại A và B .
a) chứng minh : tam giác AOM = tam giác BOM và suy ra OA=OB
b) AB cắt đường phân giác ot tại I . chứng minh IA=IB
bài 1 cho Ot là tia phân giác của góc nhọn xOy. trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. trên tia Ot lấy diểm M sao cho OM>OA.
a, chứng minh tam giác AOM=tam giác BOM
b. gọi C là giao điểm tia AM và tia Oy, gọi D là giao điểm của tia BM và tia Ox. chứng minh: Ac=BD
c. nối A và B, vẽ đường thẳng d vuông góc với AB tại A. chứng minh d // Ot
bài 2 cho góc nhọn xOy. lấy điểm A thuộc tia Ox, lấy điểm B thuộc tia Oy sao cho OA=OB. qua A kẻ đường thẳng vuông góc với Ox cắt Oy tại M. qua B kẻ đường thẳng vuông góc với Oy cắt Ox tại N. gọi H là là giao điểm của AM và BN, I là trung của MN.chứng minh rằng
a. ON=OM và AN=BM
b. tia OH là tia phân giác của góc xOy
c. đường thẳng qua B // AC cắt tia DN tại N
chứng minh: tam giác ABM=tam giác CNM
7 ) Cho Ỏt là tia phân giác của góc ^ xOy ( xOy là góc nhọn ) . Lấy I bất kỳ thuộc Ot qua I kẻ IA vuông góc Ox tại A và AI cắt Oy tại D . Qua I kẻ IB cắt Ox tại C
a ) cmr Tam giác OIA = Tam giác OIB
b ) cmr Tam giác OIC =Tam giác OID , OC= OD
c )OI vuông góc CD
d ) Cho xOy = 60 độ ; OI = 8 cm . Tính OA
Bài 1. Cho góc xOy nhọn. Kẻ tia phân giác Ot của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với tia Ox và cắt tia Ot tại C.
a) Chứng minh tam giác AOC = tam giác BOC.
b) Chứng minh CB I Oy.
c) Chứng minh OC là đường trung trực của đoạn thẳng AB.
d) Kẻ BI | Ox tại I, BI cắt OC tại H. Kẻ HK I Oy tại K. Chứng minh 3 điểm A, H, K thẳng hàng.
e) Giả sử góc xOy = 60° và OH = 3m. Tính khoảng cách từ điểm H tới hai cạnh Ox và Oy.
Từ một điểm I trên tia phân giác của góc nhọn xOy, kẻ IA vuông góc Ox (A thuộc Ox), kẻ IB vuông góc Oy ( B thuộc Oy). Tia AI cắt Oy tại C.
a. Chứng minh tam giác AOI = tam giác BOI
b. Chứng minh OI là đường trung trực của đoạn thẳng AB
c. Chứng minh IA <OA và OI <OC
