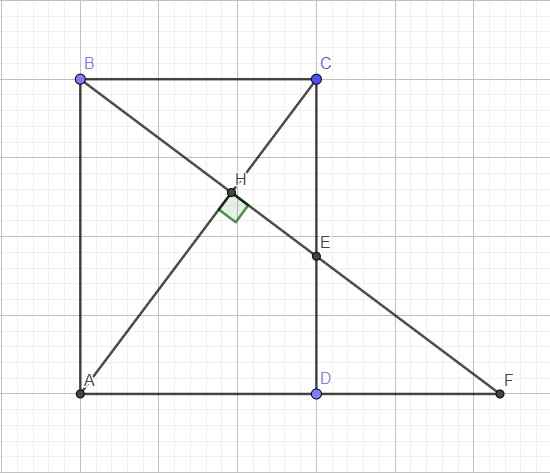
Cho hình chữ nhật ABCD, từ A hạ vuông góc với AC, cắt AC ở H. Biết rằng AB=13cm; DH=5cm. Khi đó BH=..cm (Nhập kết quả dưới dạng phân số tối giản)

Những câu hỏi liên quan
cho hình chữ nhật ABCD.Từ D hạ đường vuông góc với AC,cắt AC ở H.Biết rằng AB=13cm,DH=5cm.Tính BD
Theo đinh lý Pytago trong tam giác HCD có:
\(HC^2+HD^2=CD^2\)
\(\Rightarrow HC=\sqrt{13^2-5^2}=12\)
Lại có: \(CD^2=HC.AC\)
\(\Rightarrow13^2=12.AC\)
\(\Rightarrow AC=\frac{169}{12}\approx14,1\)
\(\Rightarrow BD\approx14,1\)(cm)
Đúng 1
Bình luận (2)
Cho hình chữ nhật ABCD. Từ D hạ đường vuông góc với AC, cắt AC ở H. Biết rằng AB=12cm ;DH=5cm.Tính đọ dài BD
ta có tam giác DHC đồng dạng với tam giác ADC
==> DC.AD = AC.DH
==> sqr(DC.AD) = SQR(AC.DH)
mà AD^2 = AC^2 - DC^2
==> 169( AC^2 - 169) = 25.AC^2
=> AC= 169/12
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD từ D hạ đường vuông góc với AC, cắt AC ở H biết rằng AB=13cm DH=5cm.Tính độ dài BD
Xét tam giác DHC vuông tại H
\(\Rightarrow HC=\sqrt{DC^2-DH^2}=12\left(cm\right)\)
Xét tam giác ADC vuông tại D đường cao DH
\(\Rightarrow AH=\dfrac{DH^2}{HC}=\dfrac{25}{12}\)
\(\Rightarrow AC=AH+HC=\dfrac{169}{12}\)(cm)
\(\Rightarrow BD=\dfrac{169}{12}\)(cm)
Đúng 0
Bình luận (0)
cho hinhf chữ nhật ABCD,từ D hạ đường vuoong góc với AC tại H .biết AB=13cm;DH=5cm .khi đó AD=...
Cho hình bình hành ABCD có AC vuông góc với AD. Qua A kẻ đường thẳng vuông góc với CD tại H và cắt BC kéo dài tại K.
a, Chứng minh rằng: CB.CK = CH.CD
b, Chứng minh rằng AH.AK + DH.DC = BC.BK
c, Biết AD = 5cm, AB = 13cm. Tính độ lớn các góc (làm tròn đến phút) và diện tích tứ giác ABCH (làm tròn đến chữ số thập phân thứ 2)
a: Ta có: AD//BC
AC\(\perp\)AD
Do đó: AC\(\perp\)BC
Xét ΔBAK vuông tại A có AC là đường cao ứng với cạnh huyền BK, ta được:
\(CB\cdot CK=AC^2\left(1\right)\)
Xét ΔADC vuông tại A có AH là đường cao ứng với cạnh huyền CD,ta được:
\(CH\cdot CD=AC^2\left(2\right)\)
Từ (1) và(2) suy ra \(CB\cdot CK=CH\cdot CD\)
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD; H là chân đường vuông góc; hạ từ B vuông AC. Gọi M,N,P là trung điểm của AB, AH, DC. Chứng minh:
a) Tứ giác MBCP là hình chữ nhật
b) BN vuông góc NP
cho tam giác vuông abc vuông góc tại a, có ab=30cm, ac=40cm, bc=50cm. từ a hạ đường cao vuông góc bc biết hc=38cm.
a,tính Stam giác:abc,abh,ahc.
b,từ h hạ đường vuông góc hd, he xuống ab,ac;tính S hình chữ nhật adhe?
trả lời nhanh hộ mình với
mình đang gấp lắm
Đúng 0
Bình luận (0)
cho tam giác vuông ABC vuông góc tại A , CÓ AB = 30 cm , AC=40 cm , BC= 50cm . Từ A hạ đường cao vuông góc BC . Biết HC= 38 m
A, Tính S tam giác ABC,ABH,AHC
b, Từ H hạ đường vuông góc HD ; HE xuống AB,AC, Tính S HÌNH CHỮ NHẬT ADHE
Cho hình chữ nhật abcd,biết AB=16,AD=12.Từ B kẻ đường thẳng vuông góc AC cắt AC và CD lần lượt tại H và E.tính ah và hc.AD và BE cắt nhau tại F.CM AD.AF=AB^2
Pitago tam giác vuông ACD:
\(AC=\sqrt{AD^2+CD^2}=\sqrt{AD^2+AB^2}=20\)
Hệ thức lượng tam giác vuông ABC với đường cao BH:
\(AB^2=AH.AC\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{64}{5}\)
\(HC=AC-AH=\dfrac{36}{5}\)
b.
Hai tam giác vuông ADC và AHF có chung góc \(\widehat{HAD}\)
\(\Rightarrow\Delta_VADC\sim\Delta_VAHF\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AC}{AF}\Rightarrow AD.AF=AC.AH\) (1)
Mặt khác theo hệ thức lượng tam giác vuông ABC:
\(AB^2=AH.AC\) (2)
(1);(2) \(\Rightarrow AD.AF=AB^2\)
Đúng 3
Bình luận (0)