a/

\(BH\perp AC\Rightarrow HF\perp AC;ME\perp AC\) => ME//HF

\(AC\perp AB\Rightarrow EH\perp HF;MF\perp BH\Rightarrow MF\perp HF\) => EH//MF

=> MEHF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => ME=HF (cạnh đối hbh)

b/

\(\widehat{BMD}+\widehat{ABC}=90^o\)

\(\widehat{CME}+\widehat{ACB}=90^o\)

\(\widehat{ABC}=\widehat{ACB}\) (góc ở đáy tg cân)

\(\Rightarrow\widehat{BMD}=\widehat{CME}\)

Mà \(\widehat{CME}=\widehat{CBH}\) (góc đồng vị)

\(\Rightarrow\widehat{BMD}=\widehat{CBH}\)

Xét tg vuông DBM và tg vuông FMB có

\(\widehat{BMD}=\widehat{CBH}\) 

BM chung 

=> tg DBM = tg FMB (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)

c/

Ta có ME = HF (cmt)

tg DBM = tg FMB (cmt) => MD = BF

=> MD+ME=BF+HF=BH không đổi

d/

Từ D dựng đt // AC cắt BC tại N

\(\Rightarrow\widehat{BND}=\widehat{ACB}\) Góc đồng vị)

\(\widehat{ABC}=\widehat{ACB}\)

=> \(\widehat{BND}=\widehat{ABC}\) => tg DBN cân tại D => BD=ND (1)

tg DBM = tg FMB (cmt) => BD=MF (2)

Mà MF = EH (cạnh đối hbh) (3)

Mà EH = KC (4)

Từ (1) (2) (3) (4) => ND = KC

Mà ND//AC => ND//KC

=> DEKN là hbh (Tứ giác có 1 cặp cạnh đối // và bằng nhau là hbh)

Mà DK và NC là hai đường chéo của hbh cắt nhau tại trung điểm mỗi đường => trung điểm của KD nằm trên NC mà NC thuộc BC => trung điểm KD nằm trên BC

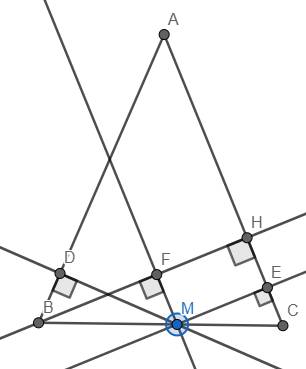
a) Vẽ MH, rõ ràng HEMF có tổng số đo của 4 góc là 360^o (vì tổng số đo của 4 góc đó là tổng số đo của các góc của các tam giác FMH và EMH)

Mà theo giả thuyết \(MD\perp AB\), \(ME\perp AC\) và \(MF\perp BH\) nên \(MF\perp ME\). Suy ra HEMF là hình chữ nhật, từ đó ME = HF.

b) Ta có \(\widehat{ABM}=\widehat{ACM}\) (vì tam giác ABC cân tại A) và \(\widehat{FMB}=\widehat{ACM}\) (vì hai góc đồng vị và AC//MF vì \(ME\perp AC\) và \(MF\perp ME\)), suy ra \(\widehat{ABM}=\widehat{FMB}\).

Xét tam giác DBM vuông tại D và FMB vuông tại F có BM là cạnh chung và \(\widehat{ABM}=\widehat{FMB}\), suy ra ΔDBM = ΔFMB (cạnh huyền - góc nhọn)

c) Từ a) và b) suy ra MD = BF, MD + ME = BF + FH = BH. Vậy khi M chạy trên đáy BC thì tổng MD + ME có giá trị không đổi.

a) xét 2 tam giác vuông AIB và AIC có:

            AI cạnh chung

          AB=AC(gt)

=> tam giác AIB=tam giác AIC(cạnh huyền-cạnh góc vuông)

=> IB=IC=> I là trung điểm của BC

b) xét 2 tam giác vuông MIB và NIC có:

      IB=IC(theo câu a)

      \(\widehat{B}\)=\(\widehat{C}\)(gt)

=> tam giác MIB =tam giác NIC(CH-GN)

=> MB=NC mà AB=AC=> AM=AN

=> tam giác AMN cân tại A

c)

bn tham khảo ở đây nha:http://text.123doc.org/document/658748-6-bai-toan-hinh-4-de-thi-ki-i-toan-8.htm

a/

Xét tg ABM và tg ACM có

MB=MC (đề bài)

AB=AC (Do tg ABC cân tại A)

\(\widehat{ABC}=\widehat{ACB}\) (Do tg ABC cân tại A)

=> tg ABM=tg ACM (c.g.c)

Ta có MB=MC => AM là trung tuyến của tg ABC => \(AM\perp BC\) (trong tg cân đường trung tuyến đồng thời là đường cao)

b/

Xét tg vuông BME và tg vuông CMF có

MB=MC

\(\widehat{ABC}=\widehat{ACB}\)

=> tg BME = tg CMF (hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => ME=MF => tg EMF cân tại M

c/

Do \(AM\perp BC\Rightarrow\widehat{AMB}=\widehat{AMC}=90^o\)

Do tg BME = tg CMF \(\Rightarrow\widehat{BME}=\widehat{CME}\)

\(\Rightarrow\widehat{AME}=\widehat{AMF}\) (cungf phụ với \(\widehat{BME}\) = \(\widehat{CMF}\) )

=> AM là phân giác của \(\widehat{FME}\Rightarrow AM\perp EF\)  (Trong tg can EMF đường phân giác đồng thời là đường cao)

Mà \(AM\perp BC\)

=> EF//BC (cùng vuông góc với AM)

a: Xét tứ giác AEMF có 

\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)

Do đó: AEMF là hình chữ nhật

a: Xét ΔABH vuông tai H và ΔACH vuông tại H có

AB=AC
AH chung

=>ΔAHB=ΔAHC

b: Xét ΔABC co

AH,CN là trung tuyến

AH cắt CN tại G

=>G là trọng tâm

c: Xét ΔABC có

H là trung điểm của CB

HE//AB

=>E là trung điểm của AC

=>B,G,E thẳng hàng