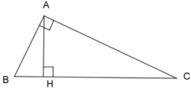
Cho tam giác ABC vuông tại A có đường cao AH,BH=16cm;CH=9cm
a) Tính AH
b)Tính AB,AC
c)AB2=BH.HC
d) Gọi M và N là trọng điểm của AH và BH;Chứng minh △ ANB ∼△CMA

Những câu hỏi liên quan
1. Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH. Biết BC = 25cm, AH = 12cm. Tính AB, AC, BH, CH
2. Cho tam giác ABC vuồng tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính AC, BC, AH, BH
cho ta m giác ABC vuông tại A có AB=12cm;AC=16cm .vẽ đường cao AH
a,CM tam giác HBA~ABC
b, tính BC; AH; BH
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7.2\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường cao AH. Biết BH=9cm, CH=16cm. Tính độ dài AH ???
Cho tam giác ABC vuông tại A có AB =12cm , AC=16cm . Vẽ đường cao AH a, chứng minh tam giác HBA đồng dang với tam giác ABC b, Tính BC,BH c, tính diện tích tam giác ABC
a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng vơi ΔABC
b: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=7,2cm
c: \(S_{ABC}=\dfrac{1}{2}\cdot12\cdot16=6\cdot16=96\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH(H € BC) biết BH=9cm CH=16cm. Tính độ dài và diện tích tam giác ABC
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=150\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH(H € BC) biết BH=9cm CH=16cm. Tính độ dài và diện tích tam giác ABC
\(S_{BAC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=150\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác vuông ABC vuông tại A; đường cao AH.Biết BH=9cm; CH=16cm. Tính độ dài AH
AH^2=BH.CH=9.16=144
suy ra AH=12 và là đáp án đấy
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 12cm, AC =16cm. Vẽ đường cao AH.
a) Cm tam giác HBA đồng dạng tam giác ABC.
b) Tính BC,AH,BH.
c)Vẽ đường phân giác AD của tam giác ABC( D thuộc BC).Tính BD,CD
Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \(\sqrt{400}\)= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \(\frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}\)
=> AH = \(\frac{12.16}{20}=9,6\)( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \(\sqrt{51,84}\) = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
\(\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}\)
<=> \(\frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}\)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \(\frac{320}{28}\approx11.43\left(cm\right)\)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \(\frac{320}{28}\)\(\approx\) 8,57 ( cm )
Đúng 0
Bình luận (0)
Cho hỏi đồng dạng là sao bạn???Tớ mới học lớp 7 thôi,nên chưa biết ^^
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Cho tam giác ABC vuông ở A, đường cao AH 16cm, BH 8cm. Tính diện tích tam giác ABC. A. 320
c
m
2
B. 300
c
m
2
C. 150
c
m
2
D. 200
c
m
2
Đọc tiếp
Cho tam giác ABC vuông ở A, đường cao AH = 16cm, BH = 8cm. Tính diện tích tam giác ABC.
A. 320 c m 2
B. 300 c m 2
C. 150 c m 2
D. 200 c m 2
Ta có: A H 2 = HB.HC (cmt)
=> 16 2 = 8.HC => HC = 32cm
=> BC = BH + HC = 8 + 32 = 40 cm
Nên diện tích tam giác ABC là S A B C = 1 2 .AH.BC = 1 2 .16.40 = 320cm2
Đáp án: A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 49cm, HC=16cm
Tính góc B,C

















