Cho ΔABC có diện tích S, BC=a; CA=b
sao cho \(\cot A+\cot B=\dfrac{a^2+b^2}{2S}\)
Chứng minh ΔABC vuông
Cho ΔABC vuông cân tại A , có cạnh BC =3a . Hảy tính diện tích ΔABC.
\(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{\dfrac{9a^2}{2}}=\sqrt{\dfrac{18a^2}{4}}=\dfrac{3a\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{18a^2}{4}:2=\dfrac{18a^2}{8}=\dfrac{9a^2}{4}\)
cho ΔABC có AB=c, BC=a, CA=b. diện tích ΔABC là 5 cm2. tìm GTNN của biểu thức a2+2b2+3c2
Cho ΔABC có diện tích S, BC=a; CA=b
sao cho
cot
A
+
cot
B
=
a
2
+
b
2
2
S
cotA+cotB=a2+b22S
Chứng minh ΔABC vuông
Sao cho cot A +cot B= a²+b²/2S
Giúp iem với iem tặng 3sp
ghi xuống hàng vầy sao đọc
* Cho ΔABC vuông tại A có B= \(30^0\), AB=6cm
a. Giải ΔABC
b. Vẽ đường cao AH và trung tuyến AM của ΔABC. Tính diện tích ΔAHM
* Cho ΔABC vuông tại A có AB=3 cm, BC=5cm, đường cao AH
a. Tính số đo góc B, C
b. Gọi AE là phân giác của góc A (E ∈ BC). Tính AE
Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)
Cho ΔABC: góc A = 90o, AH⊥BC. Tính diện tích ΔABC. Biết AH = 12cm, BH= 9cm
BC=9cm chứ?
`S_{DeltaABC}=(AH.BC)/2=(12.9)/2=6.9=54cm^2`
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow CH=\dfrac{12^2}{9}=\dfrac{144}{9}=16\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=\dfrac{300}{2}=150\left(cm^2\right)\)
Cho ΔABC có AB=2; BC=3;AC=6 a) Tính diện tích ΔABC=? b) Tính độ dài đường trung tuyến kẻ từ C c) Tính bán kính đường tròn ngoại tiếp ΔABC d) Tính số đo góc lớn nhất trong ΔABC.
AB+BC<AC
nên ko có tam giác ABC thỏa mãn nha bạn
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng k=\(\dfrac{3}{2}\) . Diện tích ΔABC là 27 cm\(^2\), thi diện tích ΔDEF là:
A. 12cm\(^2\) B.24cm\(^2\) C. 36cm\(^2\) D. 18cm\(^2\)
2) ΔABC ∼ΔDEF có AB=3cm, AC=5cm, BC=7cm, DE=6cm. Ta có :
A. DF=10cm B. DF=20cm C. EF=14cm D.EF=10cm
Cho ΔABC, điểm M nằm trên cạnh BC sao cho BC gấp 5 lần BM;
Điểm N trên cạnh AC sao cho AN = 3/4 AC.
a) Tính diện tích ΔMNC, biết diện tích ΔABC bằng 35 cm2.
b) Lấy điểm P trên đoạn MN sao cho NP = 2/3 NM. So sánh diện tích ΔAMP và ΔABM.
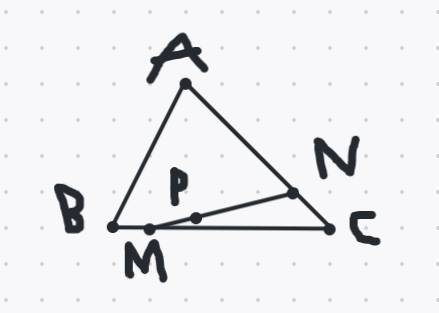
ai đó giúp mình giải với, nhanh ;-;
a/ Ta có
\(BC=5xBM\Rightarrow BM=\dfrac{1}{5}xBC\Rightarrow CM=BC-BM=BC-\dfrac{1}{5}xBC=\dfrac{4}{5}xBC\)
\(AN=\dfrac{3}{4}xAC\Rightarrow CN=AC-AN=AC-\dfrac{3}{4}xAC=\dfrac{1}{4}xAC\)
Hai tg AMC và tg ABC có chungg đường cao từ A->BC nên
\(\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{CM}{BC}=\dfrac{4}{5}\Rightarrow S_{AMC}=\dfrac{4}{5}xS_{ABC}\)
Hai tg ACM và tg MNC có chung đường cao từ M->AC nên
\(\dfrac{S_{MNC}}{S_{AMC}}=\dfrac{CN}{AC}=\dfrac{1}{4}\Rightarrow S_{MNC}=\dfrac{1}{4}xS_{AMC}=\dfrac{1}{4}x\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}=\dfrac{1}{5}x35=7cm^2\)
b/
\(S_{AMN}=S_{AMC}-S_{MNC}=\dfrac{4}{5}xS_{ABC}-\dfrac{1}{5}xS_{ABC}=\dfrac{3}{5}xS_{ABC}\)
Ta có
\(NP=\dfrac{2}{3}xNM\Rightarrow MP=NM-NP=NM-\dfrac{2}{3}xNM=\dfrac{1}{3}xNM\)
Hai tg AMP và tg AMN có chung đường cao từ A->NM nên
\(\dfrac{S_{AMP}}{S_{AMN}}=\dfrac{MP}{NM}=\dfrac{1}{3}\Rightarrow S_{AMP}=\dfrac{1}{3}xS_{AMN}=\dfrac{1}{3}x\dfrac{3}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
Ta có
\(S_{ABM}=S_{ABC}-S_{ACM}=S_{ABC}-\dfrac{4}{5}xS_{ABC}=\dfrac{1}{5}xS_{ABC}\)
\(\Rightarrow S_{AMP}=S_{ABM}\)