Gieo hai con súc sắc xanh, đỏ. Gọi x, y là số nút xuất hiện ra hột xanh và đỏ. Gọi A, B là hai biến cố sau đây.
A={(x;y)/x ⋮ y}; B={(x;y)/ 3 ≤ x+y ≤ 8}.
Tìm ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Gieo hai con súc sắc xanh, đỏ. Gọi x, y là số nút xuất hiện ra hột xanh và đỏ. Gọi A, B là hai biến cố sau đây. A = ( x ; y ) / x ⋮ y , B = ( x ; y ) / 3 ≤ x + y ≤ 8 . Tìm P(A∪B)
A. 19 24
B. 59 72
C. 29 36
D. 5 6
Gieo hai hột súc sắc màu xanh và trắng. Gọi x là số nút hiện ra trên hột xanh và y là số nút hiện ra trên hột trắng. Gọi A là biến cố (x<y) và B là biến cố 5 <x+y< 8. Khi đó ![]() có giá trị là:
có giá trị là:
A. 11/8
B. 2/3
C. 3/4
D. 7/12
Gieo hai hột súc sắc màu xanh và trắng. Gọi x là số nút hiện ra trên hột xanh và y là số nút hiện ra trên hột trắng. Gọi A là biến cố (x<y) và B là biến cố 5<x+y<8. Khi đó P ( A ∪ B ) có giá trị là
A. 11/8
B. 2/3
C. 3/4
D. 7/12
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu x + y ≥ 5 thì bốc ra 2 bi từ bình 1, còn nếu x+y < 5 thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. 29/36
B. 5/6
C. 13/72
D. 59/72
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu ![]() thì bốc ra 2 bi từ bình 1, còn nếu
thì bốc ra 2 bi từ bình 1, còn nếu ![]() thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án D
Kết quả gieo hai hột súc sắc đỏ thì không gian mẫu có 36 cặp ![]() trong đó chỉ có 6 cặp
trong đó chỉ có 6 cặp ![]() có tổng nhỏ hơn 5. Đó là
có tổng nhỏ hơn 5. Đó là ![]()
![]()
Bình 1 đựng 6 bi xanh và 4 bi vàng
=> xác suất bốc cả 2 bi vàng từ bình là ![]()
Bình 2 đựng 3 bi xanh và 6 bi vàng
=> xác suất bốc được ít nhất 1 bi xanh từ bình 2 là 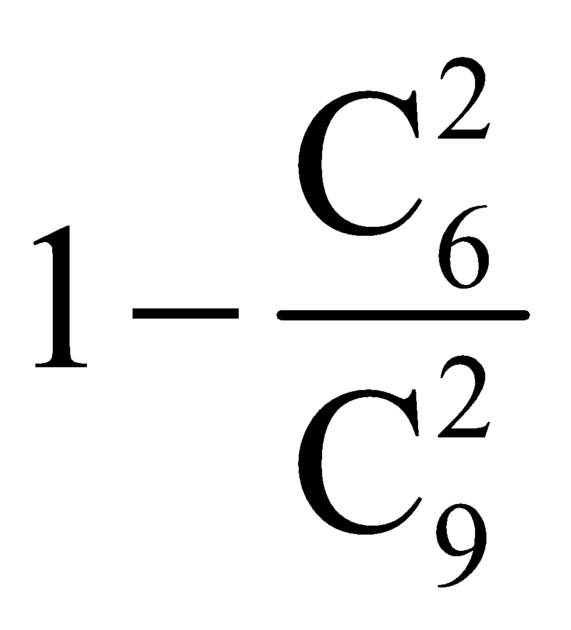
Do đó xác suất để bốc được ít nhất 1 bi xanh trong trò chơi là 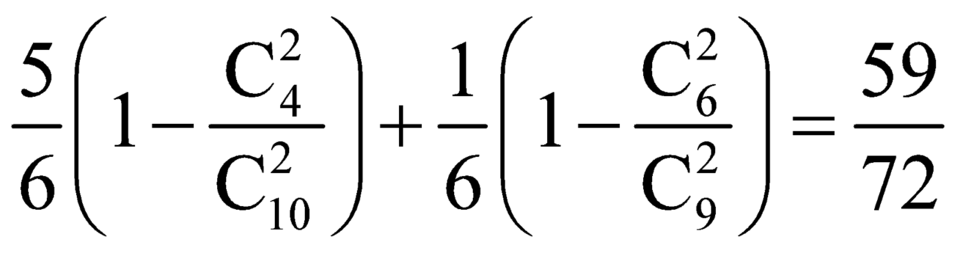
Gieo 2 con xúc sắc ngẫu nhiên 1 xanh 1 đỏ. Gọi x là số chấm trên con xúc sắc xanh, y là số chấm trên con xúc sắc đỏ. Tính xác suất của các biến cố sau:
a, A:" x lẻ và y chẵn";
b, B: " x + y = 7";
c, C:" x>y"
Lời giải:
Gieo đồng thời 2 con xúc xắc, mỗi con 6 mặt thì có $6.6=36$ kết quả (không gian mẫu)
a) Có 3 khả năng để $x$ lẻ (1, 3, 5) và 3 khả năng để $y$ chẵn (2,4,6)
Do đó số khả năng để $x$ lẻ và $y$ chẵn là $3.3=9$
Xác suất xảy ra biến cố A là: $\frac{9}{36}=\frac{1}{4}$
b)
Để $x+y=7$ thì có các khả năng là $(x,y)=(1,6), (2,5), (3,4), (4,3), (5, 2), (6,1)$, tức là có 6 khả năng xảy ra
Do đó xác suất để xảy ra biến cố B là: $\frac{6}{36}=\frac{1}{6}$
c)
$x>y$ có các khả năng là:
$(2,1); (3,1); (3,2); (4,1); (4,2); (4,3); (5,1); (5,2); (5,3); (5,4); (6,1); (6,2); (6,3); (6,4); (6,5)$, tức là có $15$ khả năng xảy ra
Xác suất biến cố C: $\frac{15}{36}=\frac{5}{12}$
Gieo hai con xúc xắc cân đối và đồng chất. Gọi \(A\) là biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 5”, gọi \(B\) là biến cố “Xuất hiện hai mặt có củng số chấm”. Hai biến cố \(A\) và \(B\) có thể đồng thời cùng xảy ra không?
THAM KHẢO:
Hai biến cố A và B không thể đồng thời cùng xảy ra.
Tung 1 con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi A là biến cố ‘tổng số chấm xuất hiện ở hai lần tung là một số nhỏ hơn 10’. Xác suất của biến cố A là
A. 1 6
B. 5 6
C. 31 36
D. 32 36
Không gian mẫu: n Ω = 6 . 6 = 36
Gọi A là biến cố: ‘‘Tổng số chấm xuất hiện hai lần tung là một số nhỏ hơn 10’’.
⇒ A ¯ : ‘‘Tổng số chấm xuất hiện hai lần tung là một số không nhỏ hơn 10’’.
Tổng số chấm là một số không nhỏ hơn 10 nên số chấm xuất hiện là các cặp:
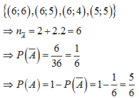
Chọn B.
Gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp. Gọi a,b,c lần lượt là số chấm xuất hiện ở 3 lần gieo. Xác suất của biến cố “ số a b c ¯ chia hết cho 45” là
A . 1 216
B . 1 54
C . 1 72
D . 1 108
Chọn C
Không gian mẫu: “ gieo ngẫu nhiên một con súc sắc 3 lần liên tiếp”
![]()
Biến cố A: “ số a b c ¯ chia hết cho 45”
a b c ¯ chia hết cho 45 ⇔ a b c ¯ chia hết cho cả 5 và 9
Vì
a
b
c
¯
chia hết cho 5 nên ![]() là số chấm xuất hiện của súc sắc khi gieo).
là số chấm xuất hiện của súc sắc khi gieo).
Vì a b c ¯ chia hết cho 9 mà c = 5 => a + b + 5 chia hết cho 9.
Các cặp số (a;b) sao cho ![]() mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
mà a+b+5 chia hết cho 9 là: (1;3), (3;1), (2;2)
Do đó: n(A) = 3.
