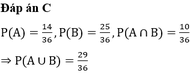Các câu hỏi tương tự
Gieo hai hột súc sắc màu xanh và trắng. Gọi x là số nút hiện ra trên hột xanh và y là số nút hiện ra trên hột trắng. Gọi A là biến cố (x<y) và B là biến cố 5<x+y<8. Khi đó P ( A ∪ B ) có giá trị là
A. 11/8
B. 2/3
C. 3/4
D. 7/12
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu
x
+
y
≥
5
thì bốc ra 2 bi từ bình 1, còn nếu x+y 5 thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh. A. 29/36 B. 5/6 C. 13/72 D. 59/72
Đọc tiếp
Gieo hai hột xúc sắc xanh và đỏ. Gọi x, y là kết quả số nút của hai hột xúc sắc đó. Có 2 bình, bình 1 đựng 6 bi xanh và 4 bi vàng, bình 2 đựng 3 bi xanh và 6 bi vàng. Nếu x + y ≥ 5 thì bốc ra 2 bi từ bình 1, còn nếu x+y < 5 thì bốc ra 2 bi từ bình 2. Tính xác suất để bốc được ít nhất một bi xanh.
A. 29/36
B. 5/6
C. 13/72
D. 59/72
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số
y
f
1
(
x
)
;
y
f
2
(
x
)
(liên tục trên [a;b]) và hai đường thẳng
x
a
,
x
b
(
a
b...
Đọc tiếp
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số y = f 1 ( x ) ; y = f 2 ( x ) (liên tục trên [a;b]) và hai đường thẳng x = a , x = b ( a < b ) . Khi đó S được tính theo công thức nào sau đây?
A. S = ∫ a b f 1 x − f 2 ( x ) d x
B. S = ∫ a b f 1 x − f 2 ( x ) 2 d x
C. S = ∫ a b f 1 ( x ) − f 2 ( x ) d x
D. S = ∫ a b f 1 ( x ) − f 2 ( x ) d x
Tung 1 con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi A là biến cố ‘tổng số chấm xuất hiện ở hai lần tung là một số nhỏ hơn 10’. Xác suất của biến cố A là A.
1
6
B.
5
6
C.
31
36
D.
32
36
Đọc tiếp
Tung 1 con súc sắc cân đối và đồng chất hai lần liên tiếp. Gọi A là biến cố ‘tổng số chấm xuất hiện ở hai lần tung là một số nhỏ hơn 10’. Xác suất của biến cố A là
A. 1 6
B. 5 6
C. 31 36
D. 32 36
Cho hai hàm số yf(x) và yg(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số yf’(x) là đường cong nét đậm, đồ thị hàm số yg’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của yf’(x) và yg’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [a;c] A.
m
i
n
h
x...
Đọc tiếp
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho hàm số yf(x) và yg(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số yf(x) , yg(x) và hai đường thẳng x a, x b(a b) Diện tích của D được tính theo công thức A.
S
∫
a
b
f
x
-
g
x
d
x
B. ...
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị các hàm số y=f(x) , y=g(x) và hai đường thẳng x= a, x= b(a < b) Diện tích của D được tính theo công thức
A. S = ∫ a b f x - g x d x
B. S = ∫ a b f x - g x d x
C. ∫ a b f x d x - ∫ a b g x d x
D. S = ∫ b a f x - g x d x
Đường thẳng d: y x - 5 cắt đồ thị (C): y
x
+
1
x
-
3
tại hai điểm A, B phân biệt. Gọi
d
1
,
d
2
lần lượt là khoảng cách từ A và B đến đường thẳng
∆
:
x
0
....
Đọc tiếp
Đường thẳng d: y = x - 5 cắt đồ thị (C): y = x + 1 x - 3 tại hai điểm A, B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng ∆ : x = 0 . Tính d = d 1 + d 2
A. d = 9
B. d = -1
C. d = 5
D. d = 5 2
Đường thẳng
d
:
y
x
-
3
cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi
d
1
,
d
2
lần lượt là khoảng cách từ A và B đến đường th...
Đọc tiếp
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số
y
f
1
x
;
y
f
2
x
(liên tục trên
a
,
b
) và hai đường thẳng
x
a
,
x
b
a
b...
Đọc tiếp
Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số y = f 1 x ; y = f 2 x (liên tục trên a , b ) và hai đường thẳng x = a , x = b a < b . Khi đó S được tính theo công thức nào sau đây?
A. S = ∫ a b f 1 x − f 2 x d x .
B. S = ∫ a b f 1 x − f 2 x 2 d x .
C. S = ∫ a b f 1 x − f 2 x d x .
D. S = ∫ a b f 1 x − f 2 x d x .