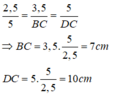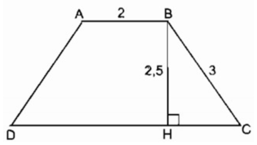
Cách dựng:

- Dựng ∆ BHC, BH = 2,5 cm

- ∠ (BHC) = 90 0

- Trên tia Hx lấy điểm C sao cho BC = 3cm

- Dựng tia đi qua B và song song CH nằm trên nửa mặt phẳng bờ BC chứa điểm H. Lấy điểm A sao cho BA = 2cm

- Dựng cung tròn tâm B bán kính bằng AC cắt tia CH tại D.

Nối AD ta có hình thang ABCD cần dựng.

Chứng minh: Thật vậy theo cách dựng AB // CD nên tứ giác ABCD là hình thang có AB = 2cm, BC = 3cm, BH = 2,5cm.

AC = BD

Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)

⇔ AB = DM và AB // DM

Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.

b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC

c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2

Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)

d) Ta có :

Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)

⇒ BC = AM = 3 (cm)

Ta có:

M là trung điểm của DC nên

SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)

Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)

⇔ SABD = SBMD = 3 (cm2)

Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)

Mày N Mày Chết M Mày Đi Kêu Cặk

a: Xét ΔADB và ΔBCD có 

\(\widehat{BAD}=\widehat{DBC}\)

\(\widehat{ABD}=\widehat{BDC}\)

Do đó: ΔADB\(\sim\)ΔBCD
b: ta có:ΔADB\(\sim\)ΔBCD

nên AD/BC=AB/BD

=>2,5/BC=1/2

hay BC=5(cm)

a: Xét ΔADB và ΔBCD có

góc DAB=góc CBD

góc ABD=góc BDC

=>ΔADB đồng dạng với ΔBCD

b: ΔADB đồng dạng với ΔBCD

=>AD/BC=DB/CD=AB/BD

=>3,5/BC=5/CD=2,5/5=1/2

=>BC=7cm; CD=10cm

a ) Ta có : \(AB=AD=\frac{CD}{2}\)    và M là trung điểm của CD (gt)

\(\Leftrightarrow AB=DM\) và AB // DM 

Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.

b) M là trung điểm của CD nên BM là trung tuyến của \(\Delta BDC\) mà MB = MD = MC.

Do đó \(\Delta BDC\) là tam giác vuông tại B hay \(DB\perp BC\)

c) ABMD là hình thoi (cmt)  \(\Leftrightarrow\widehat{D}_1=\widehat{D}_2\) 

Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)

d) Ta có :

\(HB=HD=\frac{1}{2}BD=\frac{1}{2}.4=2\left(cm\right)\)

Xét tam giác vuông AHB, ta có :

\(AH=\sqrt{AB^2-HB^2}\) ( định lí Pitago )

          \(=\sqrt{2,5^2-2^2}=1,5\left(cm\right)\)

\(\Rightarrow AM=3\left(cm\right)\)

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)

\(\Rightarrow BC=AM=3\left(cm\right)\)

Ta có :

\(S_{BDC}=\frac{1}{2}BD.BC=\frac{1}{2}.4.3=6\left(cm^2\right)\)

M là trung điểm của DC nên

\(S_{BMD}=S_{BMC}=\frac{S_{BCD}}{2}=3\left(cm^2\right)\) 

(chung đường cao kẻ từ B và MD = MC)

Mặt khác \(\Delta ABD=\Delta MDB\) ( ABCD là hình thoi )

\(\Leftrightarrow S_{ABD}=S_{BMD}=3\left(cm^2\right)\)

Vậy \(S_{ABCD}=S_{ABD}+S_{BMD}+S_{BMC}=9\left(cm^2\right)\)

Chúc bạn học tốt !!!

Buồi

a) Xét 2 tam giác ADB và BCD có:

góc DAB = góc DBC (gt)

góc ABD = góc BDC ( so le trong )

nên tam giác ADB đồng dạng với tam giác BDC.(1)

b) Từ (1) ta có AB/BC = DB/CD = AB/BD

hay AD/BC = AB/BD ⇔ 3,5/BC = 2,5/5

➩ BC= 3,5 . 5/2,5 = 7 (cm)

ta lại có: DB/CD = AB/BD ⇔ 5/CD = 2,5/5

==> CD = 5.5/2,5 =10 (cm)

c) Từ (1) ta được:

AD/BC = DB/CD = AB/BD

hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .

ta nói tam giác ADB đồng dạng với tam giác BCD theo tỉ số đồng dạng là 1/2

mà tỉ số diện tích bằng bình phương tỉ số động dạng

do đó S ADB/ S BCD = (1/2)² = 1/4

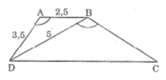
Vì △ ABD ∼  △ BDC nên: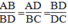 

Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có: