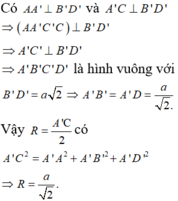Khối hộp ABCDA'B'C'D' có đáy là hình chữ nhật với AB=\(\sqrt{3}\) ; AD=\(\sqrt{7}\) . Các đường chéo AC' và DB' lần lượt tao với đáy các góc 45 hoặc 60, chiều cao của nó bằng 2, tính thể tích lăng trụ.
A.2B.4C.3D.1
Những câu hỏi liên quan
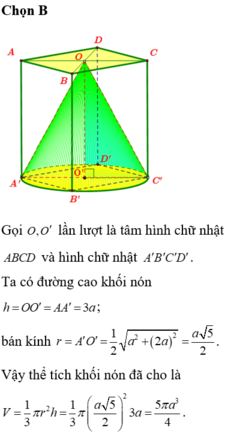
Cho hình hộp chữ nhật ABCDABCD có ABa, AD2a, AA3a. Thể tích khối nón có đỉnh trùng với tâm của hình chữ nhật ABCD, đường tròn đáy ngoại tiếp ABCD là:
Đọc tiếp
Cho hình hộp chữ nhật ABCDA'B'C'D' có AB=a, AD=2a, AA'=3a. Thể tích khối nón có đỉnh trùng với tâm của hình chữ nhật ABCD, đường tròn đáy ngoại tiếp A'B'C'D' là:
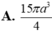
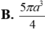
Câu 21: Cho khối hộp chữ nhật ABCD.ABCD. Biết AC5, AB7, AD8. Tính thể tích khối hộp chữ nhật này?Câu 36: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, ABa, ADasqrt{3}. SAperp(ABCD), SA2a. Gọi (P) là mặt phẳng qua A và vuông góc với cạnh bên SC, cắt các cạnh bên SB,SC,SD lần lượt tại E,F,H. Tính thể tích khối chóp S.AEFH?
Đọc tiếp
Câu 21: Cho khối hộp chữ nhật ABCD.A'B'C'D'. Biết AC=5, AB'=7, AD'=8. Tính thể tích khối hộp chữ nhật này?
Câu 36: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, \(AD=a\sqrt{3}\). SA\(\perp\)(ABCD), SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với cạnh bên SC, cắt các cạnh bên SB,SC,SD lần lượt tại E,F,H. Tính thể tích khối chóp S.AEFH?
cho hình lăng trụ ABCDA'B'C'D' đáy là hình chữ nhật tâm O. AB=a, AD=a✓3. a'o vuông góc với đáy. cạnh bên AA' tạo với đáy 1 góc 45°. tính VABCDA'B'C'D'
cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với AB=\(\sqrt{3}\),AD=\(\sqrt{7}\).hai mặt bên (ABB'A') và (ADD'A') lần lượt tạo với đáy nhưng góc 45 và 60 độ. tính thể tích khối hộp biết cạnh bên bằng 1
Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)
Đúng 0
Bình luận (0)
Cho khối hộp ABCD. ABCD có đáy là hình chữ nhật với AB
3
; AD
7
. Hai mặt bên (ABBA) và (ADDA) cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là: A.
7
B.
3
3
C. 5 D.
7
7
Đọc tiếp
Cho khối hộp ABCD. A'B'C'D' có đáy là hình chữ nhật với AB = 3 ; AD = 7 . Hai mặt bên (ABB'A') và (ADD'A') cùng tạo với đáy góc 450, cạnh bên của hình hộp bằng 1 (hình vẽ). Thể tích khối hộp là:
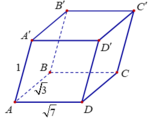
A. 7
B. 3 3
C. 5
D. 7 7
Chọn A
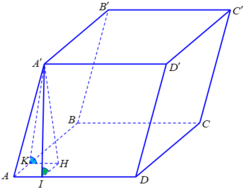
Gọi H là hình chiếu vuông góc của A' lên mặt phẳng (ABCD);

Theo giả thiết, ta có ![]()
=> ΔHKA' = ΔHIA' => HI = HK
=> tứ giác AIHK là hình vuông cạnh a, (a>0) => AH = a√2
Tam giác A'HK vuông cân tại H có HK=HA'=a
Tam giác AHA' vuông tại H có AA'²=AH²+A'H²
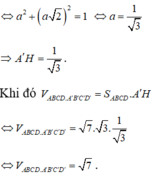
Đúng 0
Bình luận (0)
Cho khối hộp ABCD.ABCD có đáy là hình chữ nhật với
A
B
a
3
,
A
D
7
.
Hai mặt bên
A
B
B
A
v
à
A
D
D
A...
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật với A B = a 3 , A D = 7 . Hai mặt bên A B B ' A ' v à A D D ' A ' cùng tạo với đáy góc 45 0 cạnh bên của hình hộp bằng 1. Thể tích khối hộp là:
A. 7
B. 3 3
C. 5
D. 7 7
Hình hộp chữ nhật ABCDA'B'C'D' có AB=11;AD=12;AA'=13.Tính AC'.S toàn phần và V hình hộp cn
\(AC'=\sqrt{AB^2+AA'^2+AD^2}=\sqrt{11^2+12^2+13^2}=\sqrt{434}\)
S. toàn phần = 2*12*11+2*12*13+2*11*13=862
V hình hộp chữ nhật là 11*12*13=1716
****
Đúng 0
Bình luận (0)
Hình hộp chữ nhật ABCDABCD có
A
C
⊥
B
D
biết
B
D
A
A
a
. Tính diện tích S của mặt cầu ngoại tiếp hình hộp ABCDABCD
Đọc tiếp
Hình hộp chữ nhật ABCDA'B'C'D' có A ' C ⊥ B ' D ' biết B ' D ' = A A ' = a . Tính diện tích S của mặt cầu ngoại tiếp hình hộp ABCDA'B'C'D'
![]()
![]()
![]()
Một hình hộp chữ nhật có chiều cao là 90cm, đáy hình hộp là hình chữ nhật có chiều rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu? A. 68,32cm B. 78,32cm C. 58,32cm D. 48,32cm
Đọc tiếp
Một hình hộp chữ nhật có chiều cao là 90cm, đáy hình hộp là hình chữ nhật có chiều rộng là 50cm và chiều dài là 80cm. Trong khối hộp có chứa nước, mực nước so với đáy hộp có chiều cao là 40cm. Hỏi khi đặt vào khối hộp một khối trụ có chiều cao bằng chiều cao khối hộp và bán kính đáy là 20cm theo phương thẳng đứng thì chiều cao của mực nước so với đáy là bao nhiêu?
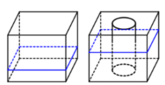
A. 68,32cm
B. 78,32cm
C. 58,32cm
D. 48,32cm
Phương pháp:
- Tính thể tích lượng nước trong khối hộp chữ nhật.
- Gọi h là chiều cao mới, lập phương trình ẩn h với chú ý lượng nước trong hộp là không đổi.
Cách giải:
Thể tích nước trước khi đưa khối trụ vào là: V n = 40.50.80 = 160000 c m 3
Gọi h là chiều cao của mực nước sau khi đặt khối trụ vào.
Khi đó thể tích khối hộp chữ nhật chiều cao h là V 1 = 50.80. h = 4000 h
Thể tích khối trụ có chiều cao h là

Đúng 0
Bình luận (0)