Cho tam giác ABC có \(\widehat{C}\)= 30o và BC=\(\sqrt{3}\);AC=2.Tính cạnh AB bằng?

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, \(\widehat{B}\) = 30o , AC= 5CM. Tính BC.
\(AC=AB=5\left(cm\right)\)
Kẻ đường cao AH thì AH cũng là trung tuyến
\(\Rightarrow BH=\dfrac{1}{2}BC=\cos B\cdot AB=\dfrac{\sqrt{3}}{2}\cdot5=\dfrac{5\sqrt{3}}{2}\\ \Rightarrow BC=2\cdot\dfrac{5\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
Đúng 3
Bình luận (1)
Cho tam giác ABC có AC=8;BC=6;C=30o . Tính độ dài cạnh AB và diện tích của tam giác AB
Xét ΔABC có
\(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{8^2+6^2-AB^2}{2\cdot6\cdot8}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(100-AB^2=48\sqrt{3}\)
=>\(AB=\sqrt{100-48\sqrt{3}}\simeq4,11\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinC\)
\(=\dfrac{1}{2}\cdot6\cdot8\cdot sin30=3\cdot8\cdot\dfrac{1}{2}=3\cdot4=12\)
Đúng 1
Bình luận (0)
\(AB=\sqrt{AC^2+BC^2-2.AC.BC.cosC}\)
\(AB=4,11\)
\(S_{ABC}=\dfrac{1}{2}. AC.BC.sinC\)
\(S_{ABC}=\dfrac{1}{2}. 8.6.sin 30^o\)
\(S_{ABC}=12\)
Đúng 1
Bình luận (0)
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
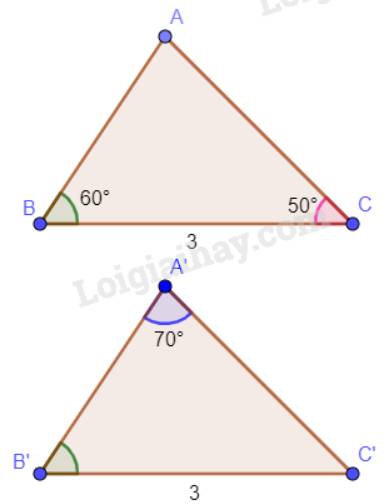
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 2 cm, góc A=105o , góc C=30o. Tính diện tích tam giác ABC.
Ta có :
góc C = 180o - 105o - 30o = 45o
Kẻ đường cao AH
Gọi BH = x(cm) $\to$ CH = 2 - x(cm)
Trong tam giác AHB vuông tại H và tam giác AHC vuông tại H, ta có :
\(AH=BH.tanB=x.tan45^o=x\\ AH=CH.tanC=\left(2-x\right).tan30^o=\dfrac{\sqrt{3}}{3}\left(2-x\right)\)
Suy ra :
\(x=\dfrac{\sqrt{3}}{3}\left(2-x\right)\Leftrightarrow x=\dfrac{2\sqrt{3}}{3+\sqrt{3}}\)
Suy ra:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2\sqrt{3}}{3+\sqrt{3}}.2\simeq0,732\left(cm^2\right)\)
Đúng 0
Bình luận (0)
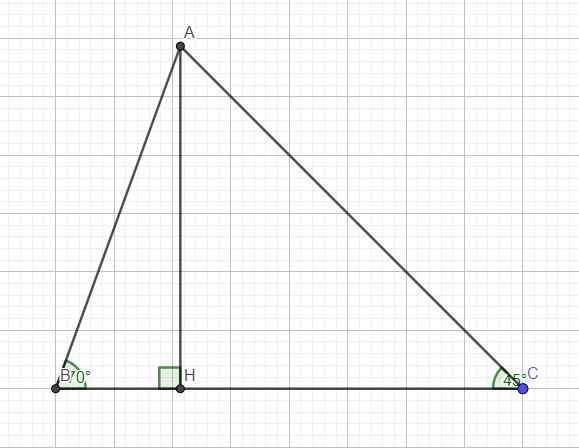
Cho tam giác ABC có BC = 4cm, \(\widehat{B}=70^o\), \(\widehat{C}=45^o\). Tính độ dài AC và diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Bài 3: Cho tam giác ABC có góc B = 80o, góc C = 30o. Tia phân giác của góc A cắt BC tại D. Tính
cho tam giác ABC có \(\widehat{B}=45^0,\widehat{C}=30^0\),BC =\(\frac{4}{\sqrt{3}-1}\)cm. Tính độ dài đường cao AH
Bài 3: Cho tam giác ABC có góc B = 80o, góc C = 30o. Tia phân giác của góc A cắt BC tại D. Tính ADC,ADB
Tam giác ABC có:
góc BAC + góc B + góc C = 180 độ
=> góc BAC + 80 độ + 30 độ = 180 độ
=> góc BAC = 180 độ - ( 80 độ + 30 độ) =70 độ
Vì AD là tia phân giác của góc BAC nên:
góc BAD = góc BAC / 2 = 70/2 = 35 độ
Vì góc ADC là góc ngoài của tam giác ADB nên:
góc ADC = góc B + góc BAD
= 80 độ + 35 độ =115 độ
Ta có: góc ADB + góc ADC = 180 độ ( kề bù)
=> góc ADB = 180 độ - góc ADC
= 180 độ - 115 độ = 65 độ
Vậy góc ADC = 115 độ, góc ADB = 65 độ
chúc em học tốt !
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đường cao AH : 3x-y+8=0 và đường trung tuyến AM: 3x+y-2=0 . Biết H, M thuộc BC ,\(\widehat{BAH}=\widehat{MAC}\) và \(BC=3\sqrt{10}\) . Viết phương trình tổng quát của đường thẳng BC.