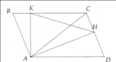
Cho hình bình hành ABCD (góc A > 900 ; AB > BC). Qua C dựng đường thẳng vuông góc BC, trên đó lấy M, N sao cho CM = CN = CB. Qua C dựng đường thẳng vuông góc với CD, trên đó lấy điểm P, Q sao cho CP = CQ = CD. (M và P nằm cùng phía đối với BC)
Chứng minh rằng AC vuông góc với MP.

Những câu hỏi liên quan
Bài 2: Cho hình bình hành ABCD có AD= 2 AD. Gọi M là trung điểm của cạnh CD. C/m:
1) AM, BM theo thứ tự là phân giác góc A và B
2) Góc AMB = 900
a) AD = DM ( gt )
⇒ ∆ ADM cân
⇒ \(\widehat{DAM}=\widehat{AMD}\)
mà \(\widehat{DAM}=\widehat{AMD}\) ( 2 góc so le trong )
⇒ \(\widehat{DAM}=\widehat{BAM}\)
⇒ AM la tia phân giác \(\widehat{A}\)
Do AD = BC (ABCD là hình bình hành)
⇒ BC = MC
⇒ △ CMB cân
⇒ \(\widehat{CMB}=\widehat{CBM}\)
mà \(\widehat{ABM}=\widehat{CMB}\) (2 góc so le trong do AB // MC)
⇒ \(\widehat{ABM}=\widehat{CBM}\)
⇒ BM là tia phân giác của \(\widehat{B}\)
b) Lấy E là trung điểm của AB
ta có AE = DM ( do AB = DC)
mà AE // DM ( do AB // CD )
⇒ Tứ giác AEDM là hình bình hành
⇒ AD = EM
mà AD =\(\dfrac{1}{2}\) AB
⇒ EM = \(\dfrac{1}{2}\) AB
⇒ ∆ AMB vuông tại M (vì trong tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông)
⇒ \(\widehat{AMB}=90^0\) ( đpcm )
Đúng 1
Bình luận (0)
1: Ta có: AB=2AD
mà AB=CD
nên CD=2AD
mà \(CD=2\cdot MD\cdot MC\)
nên AD=DM=MC=BC
Xét ΔAMD có DA=DM
nên ΔAMD cân tại D
Suy ra: \(\widehat{DAM}=\widehat{DMA}\)
mà \(\widehat{DMA}=\widehat{MAB}\)
nên \(\widehat{DAM}=\widehat{BAM}\)
hay AM là tia phân giác của \(\widehat{DAB}\)
Xét ΔBCM có MC=MB
nên ΔBMC cân tại C
Suy ra: \(\widehat{CMB}=\widehat{CBM}\)
mà \(\widehat{CMB}=\widehat{ABM}\)
nên \(\widehat{CBM}=\widehat{ABM}\)
hay BM là tia phân giác của \(\widehat{ABC}\)
Đúng 1
Bình luận (0)
2: Gọi K là trung điểm của AB
Ta có: \(AK=\dfrac{AB}{2}\)
\(DM=\dfrac{DC}{2}\)
mà AB=DC
nên AK=DM
Xét tứ giác AKMD có
AK//MD
AK=MD
Do đó: AKMD là hình bình hành
mà AD=DM
nên AKMD là hình thoi
Suy ra: MK=AK
mà \(AK=\dfrac{AB}{2}\)
nên \(MK=\dfrac{AB}{2}\)
Xét ΔMAB có
MK là đường trung tuyến ứng với cạnh AB
\(MK=\dfrac{AB}{2}\)
Do đó: ΔMAB vuông tại M
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có A = α > 90 0 . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Chứng minh rằng tam giác CEF là tam giác đều.
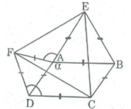
Ta có:
∠ (BAD) + ∠ ∠ (ADC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ADC) = 180 0 - ∠ (BAD) = 180 0 – α
∠ (CDF) = ∠ (ADC) + ∠ (ADF) = 180 0 - α 2 + 60 0 = 240 0 - α
Suy ra: ∠ (CDF) = ∠ (EAF)
Xét ∆ AEF và ∆ DCF: AF = DF ( vì ∆ ADF đều)
AE = DC (vì cùng bằng AB)
∠ (CDF) = ∠ (EAF) (chứng minh trên)
Do đó: ∆ AEF = ∆ DCF (c.g.c) ⇒ EF = CF (1)
∠ (CBE) = ∠ (ABC) + 60 0 = 180 0 - α + 60 0 = 240 0 - α
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
∠ (CBE) = ∠ (CDF) = 240 0 - α
BC = DF (vì cùng bằng AD)
Do đó ∆ BCE = ∆ DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ∆ ECF đều.
Đúng 0
Bình luận (0)
câu 10 cho hình bình hành ABCD (AB//GÓC D=130\(^0\)
CD và góc B - góc C =50\(^0\)hãy tính các góc còn lại của hình thang
câu 11 cho hình bình hành ABCD có góc A =3 lần góc B.Hãy tính số đo góc của hình bình hành
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD, AB= 10cm, AD= 6cm, góc A > góc B. Tính số đo các góc của hình bình hành ABCD.
mình dốt hình lắm chỉ biết số học thôi
CHÚC BẠN HỌC GIỎI
TK MÌNH NHÉ
Đúng 0
Bình luận (0)
Bài 5. Cho hình bình hành ABCD ( Â > 900). Vẽ ra ngoài hình bình hành các tam giác đều ADE và ABF. Chứng minh : rCEF là tam giác đều.
Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB=a, góc A = α . Tính diện tích hình bình hành ABCD theo a và α
Cho tứ giác ABCD là hình bình hành và B A D ⏜ = 90 0 . Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Trung điểm AC
B. Điểm A
C. Điểm B
D. Điểm D
Đáp án A
Vì tứ giác ABCD là hình bình hành và 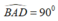 nên ABCD là hình chữ nhật.
nên ABCD là hình chữ nhật.
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
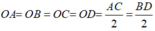
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có góc a = 3 góc B . Tính số đo các góc của hình bình hành
\(\widehat{A}=\widehat{C}=135^0\)
\(\widehat{B}=\widehat{D}=45^0\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD,
A
^
90
0
.
Kẻ
A
H
⊥
C
D
tại H,
A
K
⊥
B
C
tại K. Chứng minha)
A
H
A
K
D
A
D
C...
Đọc tiếp
Cho hình bình hành ABCD, A ^ > 90 0 . Kẻ A H ⊥ C D tại H, A K ⊥ B C tại K. Chứng minh
a) A H A K = D A D C ;
b) A K H ^ = A C H ^ .
Cho hình bình hành ABCD có góc D = α (α< 900), vẽ BH vuông góc CD, BK vuông góc AD. C/m rằng:
a) tam giác BHK đồng dạng với tam giác ABD.
b)HK=BH * sin α.
c) Tính SKBHD biết AB=26cm , AD=4cm, α=600