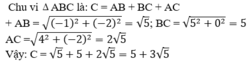Cho tam giác ABC với A(-2;7);B(1;2);C(7;9).Tìm điểm M nằm trên đường thẳng y=x sao cho T=MA2+MB2+MC2 đạt giá trị nhỏ nhất

Những câu hỏi liên quan
Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2). Hỏi tam giác ABC là tam giác gì?
A. tam giác cân
B. tam giác đều
C. tam giác nhọn
D. tam giác vuông
Chọn D.
Ta có: ![]()
suy ra ![]()
do đó; 2 vecto AB và AC vuông góc với nhau
suy ra tam giác ABC vuông tại A.
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a, đường cao ah. a)cm tam giác abc đồng dạng với tam giác hac b)kẻ hk vuông góc với ba tại k. chứng minh KH^2=KA.KB c)cho ac=10cm, ch=8cm. tính ah và diện tích tam giác abc\
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{ACB}\) chung
Do đó: ΔABC đồng dạng với ΔHAC
b: Xét ΔKHB vuông tại K và ΔKAH vuông tại K có
\(\widehat{KHB}=\widehat{KAH}\left(=90^0-\widehat{B}\right)\)
Do đó: ΔKHB đồng dạng với ΔKAH
=>\(\dfrac{KH}{KA}=\dfrac{KB}{KH}\)
=>\(KH^2=KA\cdot KB\)
c: Ta có: ΔAHC vuông tại H
=>\(HC^2+HA^2=AC^2\)
=>\(HA^2=10^2-8^2=36\)
=>\(HA=\sqrt{36}=6\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(HB=\dfrac{6^2}{8}=4,5\left(cm\right)\)
BC=BH+CH
=4,5+8
=12,5(cm)
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot12,5\cdot6=3\cdot12,5=37,5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC với A(2; 4), B(1; 2), C(6; 2).Tính chu vi tam giác ABC.
A. 5
B. 5 + 2 5
C. 5 + 3 5
D. Đáp án khác
cho tam giác abc m là trung điểm của bc d l 1 điểm trên ac sao cho ad =1/2 đc nỗi ám dm a ;so sánh tam giác amc với tam giác abc b;so sánh tam giác dmc với tam giác amc c; so sánh tam giác dmc với tam giác abc d; nôi bd so sánh tam giác mbd voi tam giac abd
Bài 1: Cho tam giác với độ dài 12m,16m,18m. Tính chu vi và các cạnh của tam giác đồng dạng với tam giác đã cho, nếu cạnh bé nhất của tam giác này là cạnh lớn nhất của tam giác đã choBài 2:Tam giác ABC có ABAC3cm, BC2cm, đường phân giác BD. Đường vuông góc với BD tại B cắt AC tại E. Tính độ dài CEBài 3: Cho tam giác ABC đồng dạng với tam giác ABC theo tỉ số đồng dạng là 2/3, tam giác ABC đồng dạng với tam giác ABC theo tỉ số đồng djng là 3/4a, Vì sao tam giác ABC đồng dạng với tam giác ABCb, Tìm...
Đọc tiếp
Bài 1: Cho tam giác với độ dài 12m,16m,18m. Tính chu vi và các cạnh của tam giác đồng dạng với tam giác đã cho, nếu cạnh bé nhất của tam giác này là cạnh lớn nhất của tam giác đã cho
Bài 2:Tam giác ABC có AB=AC=3cm, BC=2cm, đường phân giác BD. Đường vuông góc với BD tại B cắt AC tại E. Tính độ dài CE
Bài 3: Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng là 2/3, tam giác A'B'C' đồng dạng với tam giác A''B''C'' theo tỉ số đồng djng là 3/4
a, Vì sao tam giác ABC đồng dạng với tam giác A''B''C''
b, Tìm tỉ số đồng dạng của 2 tam giác đó
Bài 1: Cho tam giác với độ dài 12m,16m,18m. Tính chu vi và các cạnh của tam giác đồng dạng với tam giác đã cho, nếu cạnh bé nhất của tam giác này là cạnh lớn nhất của tam giác đã choBài 2:Tam giác ABC có ABAC3cm, BC2cm, đường phân giác BD. Đường vuông góc với BD tại B cắt AC tại E. Tính độ dài CEBài 3: Cho tam giác ABC đồng dạng với tam giác ABC theo tỉ số đồng dạng là 2/3, tam giác ABC đồng dạng với tam giác ABC theo tỉ số đồng djng là 3/4a, Vì sao tam giác ABC đồng dạng với tam giác ABCb, Tìm...
Đọc tiếp
Bài 1: Cho tam giác với độ dài 12m,16m,18m. Tính chu vi và các cạnh của tam giác đồng dạng với tam giác đã cho, nếu cạnh bé nhất của tam giác này là cạnh lớn nhất của tam giác đã cho
Bài 2:Tam giác ABC có AB=AC=3cm, BC=2cm, đường phân giác BD. Đường vuông góc với BD tại B cắt AC tại E. Tính độ dài CE
Bài 3: Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng là 2/3, tam giác A'B'C' đồng dạng với tam giác A''B''C'' theo tỉ số đồng djng là 3/4
a, Vì sao tam giác ABC đồng dạng với tam giác A''B''C''
b, Tìm tỉ số đồng dạng của 2 tam giác đó
Bài 2 :
vì BE vuông góc BD nên BE là đường phân giác ngoài của tam giác ABC.
theo tính chất đường phân giác (ngoài) ta có :
AEEB=ECBCAEEB=ECBC
⇒⇒ CE=AB.BCABCE=AB.BCAB
⇒⇒ CE=AE.23CE=AE.23
⇒⇒ 3CE=(CE+AC).23CE=(CE+AC).2
⇒⇒ 3CE=2CE+2AC3CE=2CE+2AC
⇒⇒ CE=2AC=6(cm)
Bài 1: Giải
Nếu cạnh lớn nhất của tam giác đã cho là cạnh bé nhất của tam giác đồng dạng với nó thì ta có tỉ số đồng dạng đã cho là: (Gọi tạm tam giác có cạnh 12,16,18 m là tgiac 1, tgiac mới là tgiac 2)
k=Δ1Δ2=1218=23k=Δ1Δ2=1218=23
Chu vi của tam giác 1 là:
12+16+18=46(m)12+16+18=46(m)
⇒⇒ Chu vi của tam giác 2 là: 46:23=69(m)46:23=69(m)
Cạnh thứ hai của tam giác đồng dạng (2) là:
16:23=24(m)16:23=24(m)
Cạnh lớn nhất của tam giác đồng dạng (2) đó là:
69−24−18=27(m
Bài 3 tớ k bt lm
copy mạng nhớ ghi nguồn nhé bạn =))))
học tốt bro :))
~~
cho tam giác ABC vuông tại A,đường cao AH .AB=15,AC=20.a)tam giác ABC đồng dạng với tam giác HBA suy ra AB^2=BC.BH
Xem chi tiết
Câu trả lời bằng hình

1 Cho tam giác ABC và tam giác A'B'C' có góc A = góc A' BC = B'C' góc B = B' chứng minh rằng tam giác ABC = tam giác A'B'C'
2 Cho tam giác ABC có AB = AC phân giác AD chứng minh rằng AD vuông góc với BC
AI TRA LỜI NHANH GIÚP MÌNH VỚI TvT
2. \(\Delta ABC\)có AB=AC \(\Rightarrow\Delta ABC\)cân.
AD là phân giác \(\Delta ABC\)mà \(\Delta ABC\)cân.
\(\Rightarrow AD\)l là đường trung trực \(\Delta ABC\)..
\(\Rightarrow AD\)là đường cao \(\Delta ABC\)..
\(\Leftrightarrow AD\perp BC\).
Hình 1 :
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có : Góc A = Góc A' ( gt ); \(BC=B'C'\left(gt\right)\); Góc B = Góc B' ( gt )
\(\Rightarrow\Delta ABC=\Delta A'B'C\left(ch-gn\right)\)
Hình 2 :
Vì \(\Delta ABC\) có \(AB=AC\Leftrightarrow\Delta ABC\) cân tại A . Vì AD là phân giác góc A
\(\Leftrightarrow\) ^BAD = ^CAD. Xét \(\Delta ABD\) và \(\Delta ACD\) có : \(AB=AC\left(gt\right)\); ^BAD = ^CAD; AD chung.
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\Leftrightarrow\) ^ADB = ^ADC ( tương ứng ) . Mà ^ADB + ^ADC = 1800 ( kề bù )
\(\Leftrightarrow\) ^ADB = ^ADC = 1800 : 2 = 900 nên suy ra \(AD\perp BC\)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A. Đường cao AH.
1.Chứng minh tam giác ABC đồng dang với tam giác Hac.Từ đó suy ra AC^2CH.BC
2.Chứng minh AH^2BH.HC
3. Kẻ phân giác BE của tam giác ABC,phân giác EM của tam giác AEB, phân giác En của tam giác BEC. Chứng minh: dfrac{BM}{MA}.dfrac{EA}{EC}.dfrac{CN}{BN}1
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường cao AH.
1.Chứng minh tam giác ABC đồng dang với tam giác Hac.Từ đó suy ra AC\(^2\)=CH.BC
2.Chứng minh AH\(^2\)=BH.HC
3. Kẻ phân giác BE của tam giác ABC,phân giác EM của tam giác AEB, phân giác En của tam giác BEC. Chứng minh: \(\dfrac{BM}{MA}\).\(\dfrac{EA}{EC}\).\(\dfrac{CN}{BN}\)=1
Bài 1: Cho tam giác ABC và tam giác MNP có góc A = 60 độ,AB = 4cm,AC = 9cm và góc P = 60 độ,PM = 4,5cm,PN = 2cm.Kết luận nào sau đây đúng ?
1/Tam giác ABCđồng dạng với tam giác MNP
2/Tam giác ABC đồng dạng với tam giác MPN
3/ Tam giác ABC đồng dạng với tam giác PNM
4/Tam giác ABC đồng dạng với tam giác MPN