Cho hàm số y =(f)x=(3m-2)x (d)
a) Tìm m biết I (2;8) thuộc (d)
b) Vẽ đồ thị hàm số với m tìm được ở câu a. CMR f (-2)+f (-4)=3f (-2)
cho hàm số y=f(x)=(3m-2)x
a) tìm m biết đồ thị hàm số đi qua điểm M(1,4)
b)tính f(-2) +2.f(0)-f(2)
a, Để đồ thị hàm số y=f(x)=(3m-2)x đi qua điểm M(1,4) thì:
\(4=\left(3m-2\right).1\\ \Rightarrow3m-2=4\\ \Rightarrow3m=6\\ \Rightarrow m=2\)
b, \(f\left(-2\right)+2f\left(0\right)-f\left(2\right)=\left(3m-2\right)\left(-2\right)+2\left(3m-2\right).0-\left(3m-2\right).2=4-6m+0-6m+4=8\)
cho hàm số y=f(x)=(3m-2)x a) tìm m biết đồ thị hàm số đi qua điểm M(1,4)
Do đồ thị hàm số đi qua M(1;4) nên:
\(\left(3m-2\right).1=4\)
\(\Rightarrow3m-2=4\)
\(\Rightarrow3m=6\)
\(\Rightarrow m=2\)
cho hàm số y=f(x)=(3m-2)x a) tìm m biết đồ thị hàm số đi qua điểm M(1,4)
đồ thị hàm số y=f(x)=(3m-2)x đi qua điểm M(1,4) thì:
\(4=\left(3m-2\right).1\\
\Rightarrow3m-2=4\\
\Rightarrow3m=6\\
\Rightarrow m=2\)
Cho hàm số y= f(x)=2x+3m (x là biến số). Tìm m, biết f(-2)=-1
Ta có : \(f\left(x\right)=2x+3m\)hay \(f\left(-2\right)=2\left(-2\right)+3m=-1\)
\(\Leftrightarrow-4+3m=-1\Leftrightarrow3m=3\Leftrightarrow m=1\)
Vậy m = 1
bài 1: a/ cho hàm số \(y=\frac{3}{2}x\) . điểm E ( -4;m ) là 1 điểm thuộc đồ thị của hàm số trên. tìm m.
b/ cho hàm số y=I\(m+\frac{1}{2}\)I . x-3 đi qua điểm B ( 2;-1).
c/ cho hàm số y=f(x)=(2a + 3).x + . tìm a biết f(1)=-4
bài 2: cho hàm số y=f(x)=\(-x^2\)+3x. tính f(-2), f(\(\frac{2}{3}\)).
Cho hàm số y = f(x) = (1- 3m)x. a) Tìm giá trị của m và xác định công thức của hàm số, biết đồ thị hàm số đi qua điểm ( -3 ; 24). b) Với công thức hàm số xác định được ở trên, tìm toạ độ của điểm A có hoành độ là 2 nằm trên đồ thị hàm số.
a: Thay x=-3 và y=24 vào y=(1-3m)x, ta được:
-3(1-3m)=24
=>-3+9m=24
=>m=3
Cho hàm số y = f(x) = (m+1)x – 2 có đồ thị là (d)
a. Tìm m biết rằng đồ thị (d) của hàm số đi qua A(-2:0)
b. Nêu tính chất và vẽ đồ thị hàm số với m tìm được ở câu a .
c. Không tính hãy so sánh f(2√3) và f(3√2)
d. Viết phương trình đường thẳng đi qua B(-1;1)và vuông góc với (d) nói trên
Cho hàm số \(y=f\left(x\right)=x^2+2\left(m-1\right)x+3m-5\) (m là tham số). Tìm m để giá trị nhỏ nhất của f(x) đạt giá trị lớn nhất
Dễ thấy: \(f\left(x\right)=\left(x+m-1\right)^2-m^2+5m-6\ge-m^2+5m-6\)
Giá trị nhỏ nhất của f(x) đạt lớn nhất tức \(-m^2+5m-6\) đạt lớn nhất
Mà \(g\left(m\right)=-m^2+5m-6=-\left(m-\dfrac{5}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
g(m) đạt lớn nhất khi m=5/2
m cần tìm là 5/2
cho hàm số y= f(x)=(m-3)x + m-2 a)tìm m để hàm số trên là hàm số đồng biến b) tìm m biết f(-1)=1
a: Để hàm số đồng biến thì m-3>0
hay m>3
b: Thay x=-1 và y=1 vào (d), ta được:
-m+3+m-2=1
hay 1=1(đúng)
Cho hàm số y = f (x) có bảng biến thiên như sau:
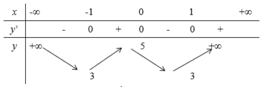
Tìm m để phương trình f (x) = 2 – 3m có bốn nghiệm phân biệt
A. m < - 1 h o ặ c m > - 1 3
B. - 1 < m < - 1 3
C. m = - 1 3
D. m ≤ - 1