30: Cho đường tròn (O;5cm) và OA = 6cm. Hãy cho biết vị trí của điểm A với (O;5cm)
Những câu hỏi liên quan
Cho đường tròn tâm O. Biết diện tích hình quạt tròn cung 30 ° l à 3 π . Tính bán kính đường tròn?
A. 6cm
B. 5cm
C. 3cm
D. 9cm
Chọn đáp án A
Diện tích hình quạt tròn cung 30° là:
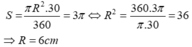
Đúng 0
Bình luận (0)
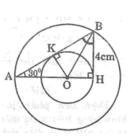
Cho tam giác AHB có góc H = 90 ° ,góc A = 30° và BH =4cm.Tia phân giác góc B cắt AH tại O. Vẽ đường tròn (O;OH) và đường tròn (O;OA). Chứng minh đường tròn (O;OH) tiếp xúc với cạnh AB
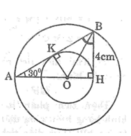Kẻ OK ⊥ AB (1)
Theo giả thiết ,OB là đường phân giác của góc B nên ta có:
OK = OH (tính chất đường phân giác) (2)
Từ (1) và (2) suy ra (O;OH) tiếp xúc với AB tại K
Đúng 0
Bình luận (0)
cho 30 điểm thuộc đường tròn tâm o và 1 điểm O không thuộc đươngd tròn tâm d.Có bao nhiêu tam giác nhận O là đỉnh và 2 đỉnh kia lag 2 trong 30 đỉnh đã cho
Cho tam giác AHB có góc H = 90 ° ,góc A = 30° và BH =4cm.Tia phân giác góc B cắt AH tại O. Vẽ đường tròn (O;OH) và đường tròn (O;OA). Tính diện tích hình vành khăn nằm giữa hai đường tròn trên
Cho đường tròn (O; 9cm). Từ điểm M nằm ngoài (O) về tiếp tuyến MA với đường tròn (A là tiếp điểm), biết MOA = 30°. Tính độ dài AM.
Xét ΔOAM vuông tại A có \(tanAOM=\dfrac{AM}{OA}\)
=>\(\dfrac{AM}{9}=tan30=\dfrac{1}{\sqrt{3}}\)
=>\(AM=\dfrac{9}{\sqrt{3}}=3\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho đường tròn (O) đường kính AB
4
3
cm. Điểm
C
∈
(
O
)
sao cho
A
B
C
^
30
°
. Tính diện tích hình viên phân AC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy ) A.
π
-
3
3
cm...
Đọc tiếp
Cho đường tròn (O) đường kính AB = 4 3 cm. Điểm C ∈ ( O ) sao cho A B C ^ = 30 ° . Tính diện tích hình viên phân AC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy )
A. π - 3 3 cm 2
B. 2 π - 3 3 cm 2
C. 4 π - 3 3 cm 2
D. 2 π - 3 cm 2
Cho đường tròn (O;R). Từ một điểm M nằm ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn (A,B là tiếp điểm) sao cho AMO = 30 độ
a, Chứng minh MO=2R
b, Tính AB theo R
c, Tính S MAB theo R
a: Xét ΔAOM vuông tại A có
\(\sin\widehat{AMO}=\dfrac{OA}{OM}\)
\(\Leftrightarrow OM=OA:\dfrac{1}{2}=2\cdot OA=2\cdot R\)
Đúng 0
Bình luận (0)
14 tháng 10 2021 lúc 15:43
cho đường tròn(O;5cm),đường kính AB,tiếp tuyến Bx với đường tròn. Gọi C là một điểm trên đường tròn sao cho góc CAB=30\(^0\), tia AC cắt tia Bx tại E
a)chướng minh BC\(^2\)=AC\(\cdot\)CE
Cho đường tròn (O; 4cm) và một điểm M sao cho MO = 8cm. Kẻ tiếp tuyến MN với đường tròn (O), N là tiếp điểm. Số đo của góc MON là:
(A) 45 °
(B) 90 °
(C) 30 °
(D) 60 °
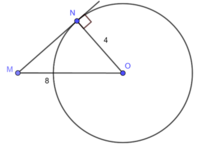
Vì MN là tiếp tuyến của đường tròn (O) tại N nên
Xét tam giác vuông MNO có:
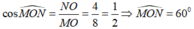
Đáp án: D
Đúng 0
Bình luận (0)
Bài 1: Cho đường tròn (O; R), đường kính AB. Vẽ dây AC sao cho góc CAB = 30. Trên tia đối của tia BA, lấy điểm M sao cho BM = R. C/m: a) MC là tiếp tuyến của đường tròn (O). b) MC^2 = 3R^2.
a: Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
mà \(\widehat{CBO}=60^0\)
nên ΔOBC đều
Xét ΔOCM có
CB là đường trung tuyến
CB=OM/2
Do đó: ΔOCM vuông tại C
hay MC là tiếp tuyến của (O)
Đúng 0
Bình luận (0)