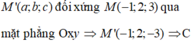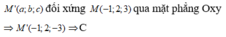Bài 2: Trong mặt phẳng hệ tọa độ Oxy cho AABC có M(0;5) là trung điểm cạnh BC. Đường thẳng
chứa cạnh AB, AC lần lượt có phương trình 2x +y-12 =0, x+4y-6=0. Tìm tọa độ 3 đỉnh của tam
giác ABC.

Những câu hỏi liên quan
trong mặt phẳng hệ tọa độ oxy,cho điểm A(2;5)B(0;-7).tọa độ diểm M của AB là
Lời giải:
Tọa độ trung điểm $M$ của $AB$ là:
\(\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)=\left(\frac{2+0}{2}; \frac{5+(-7)}{2}\right)=(1;-1)\)
Đúng 0
Bình luận (2)
Trong không gian với hệ tọa độ Oxyz, cho M(-1;2;3). Khi đó điểm M' đối xứng với M qua mặt phẳng (Oxy) có tọa độ là
A. M'(1;2;3)
B. M'(-1;-2;3)
C. M'(-1;2;-3)
D. M'(1;-2;3)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình là
x
-
z
-
3
0
. Tính góc giữa (P) và mặt phẳng (Oxy) A. 30
°
B. 60
°
C. 45
°
D. 90
°
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình là x - z - 3 = 0 . Tính góc giữa (P) và mặt phẳng (Oxy)
A. 30 °
B. 60 °
C. 45 °
D. 90 °
Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;2;3). Khi đó điểm M' đối xứng với M qua mặt phẳng (Oxy) có tọa độ là
A. M'(1;2;3)
B. M'(-1;-2;3)
C. M'(-1;2;-3)
D. M'(1;-2;3)
Trong không gian với hệ tọa độ Oxyz cho điểm M (-1;2;3). Khi đó điểm
M
đối xứng với M qua mặt phẳng (Oxy) có tọa độ là A.
M
(1;2;3) B.
M
(-1;-2;3) C.
M
(-1;2;-3) D.
M
(1;-2;3)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M (-1;2;3).
Khi đó điểm M ' đối xứng với M qua mặt phẳng (Oxy) có tọa độ là
A. M ' (1;2;3)
B. M ' (-1;-2;3)
C. M ' (-1;2;-3)
D. M ' (1;-2;3)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
a) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) có phương trình 2x-3y+1=0
Lập pt đường thẳng(d') qua M(-1',1)và song song với(d)
b)Trong mặt phẳng hệ tọa độ Oxy,cho elip có pt(E):x\(\frac{x^2}{49}+\frac{y^2}{25}=1\)
tính chu vi,diện tích hình chữ nhật của elip
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có AB :2x -y + 1 = 0, AC : x -y + 1 = 0 và M là trung điểm của CD thuộc đường thẳng 2x + y + 1 = 0 . Tìm tọa độ các đỉnh A, B, C, D