Các câu hỏi tương tự
Trong không gian Oxyz, cho điểm
M
(
1
;
2
;
3
)
. Tọa độ điểm M’ đối xứng với M qua mặt phẳng (Oxy) là
Đọc tiếp
Trong không gian Oxyz, cho điểm M ( 1 ; 2 ; 3 ) . Tọa độ điểm M’ đối xứng với M qua mặt phẳng (Oxy) là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng d:
x
-
1
+
t
y
2
+
2
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3) và đường thẳng d: x = - 1 + t y = 2 + 2 t z = 1 - 2 t . Xác định tọa độ điểm là điểm đối xứng với M qua đường thẳng d.
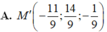
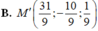
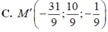
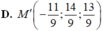
Trong không gian với hệ tọa độ Oxyz, mặt phẳng(α) đi qua điểm M(1;2;-3) và nhận (1;-2;3) làm véc-tơ pháp tuyến có phương trình là: A. x-2y-3z+60 B. x-2y-3z-60 C. x-2y+3z-120 D. x-2y+3z+120.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, mặt phẳng(α) đi qua điểm M(1;2;-3) và nhận ![]() =(1;-2;3) làm véc-tơ pháp tuyến có phương trình là:
=(1;-2;3) làm véc-tơ pháp tuyến có phương trình là:
A. x-2y-3z+6=0
B. x-2y-3z-6=0
C. x-2y+3z-12=0
D. x-2y+3z+12=0.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;-2;3). Tọa độ điểm A là hình chiếu vuông góc của điểm M trên mặt phẳng (Oyz) là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;-2;3). Tọa độ điểm A là hình chiếu vuông góc của điểm M trên mặt phẳng (Oyz) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;3). Tọa độ điểm A là hình chiếu vuông góc của điểm M lên mặt phẳng (Oyz) là: A. A(1;-2;0) B. A(0;-2;3) C. A(1;-2;3) D. A(1;0;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;3). Tọa độ điểm A là hình chiếu vuông góc của điểm M lên mặt phẳng (Oyz) là:
A. A(1;-2;0)
B. A(0;-2;3)
C. A(1;-2;3)
D. A(1;0;3).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;3). Tìm tọa độ điểm A là hình chiếu vuông góc của M lên mặt phẳng (Oyz)
A. A(1;-2;3)
B. A(1;-2;0)
C. A(1;0;3)
D. A(0;-2;3)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oyz) là điểm M. Tọa độ của điểm M là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-2;3). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oyz) là điểm M. Tọa độ của điểm M là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC A. 1372/9 B. 686/9 C. 524/3 D. 343/9
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. 686/9
C. 524/3
D. 343/9
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng cách lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Thể tích khối chóp O.ABC bằng A.
1372
9
B.
686
9
C.
524
3
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng cách lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Thể tích khối chóp O.ABC bằng
A. 1372 9
B. 686 9
C. 524 3
D. 343 9