Cho tam giác ABC có S = 45 (đvdt) , B (2;1) , C (-1;5) , trọng tâm G thuộc tam giác : x - 3y + 1 = 0 . Tìm tọa độ điểm A

Những câu hỏi liên quan
Cho A(-1; 2); B (3; -1) a) Tìm C trên Oy để S∆ABC = 3 đvdt. b) Tìm D để tam giác ABD đều.
cho mặt cầu (S): x^2 + y^2 + z^2 -2x -2y -2z =0 và điểm A(2;2;2). Điểm B thay đổi trên mặt cầu. Diện tích của tam giác OAB có giá trị lớn nhất là?
A. 1 (đvdt)
B. 2 (đvdt)
C. căn bặc hai của 3 (đvdt)
D, 3 (đvdt)
Lời giải:
Ta có:
\((S): x^2+y^2+z^2-2x-2y-2z=0\)
\(\Leftrightarrow (x-1)^2+(y-1)^2+(z-1)^2=3\)
Do đó mặt cầu \((S)\) có tâm \(O=(1,1,1)\) và \(R=\sqrt{3}\)
Khi đó, dễ dàng nhận thấy \(A\in (S)\)
Ta có \(S_{OAB}=\frac{OA.OB.\sin \angle AOB}{2}\leq \frac{OA.OB.1}{2}=\frac{3}{2}\) vì \(\sin AOB\leq 1\)
Dấu bằng xảy ra khi \(\angle AOB=90^0\)
Đúng 0
Bình luận (1)
Cho lăng trụ tam giác đều ABC.ABC có diện tích đáy bằng
a
2
3
(đvdt), diện tích tam giác ABC bằng
2
a
2
(đvdt). Tính góc giữa hai mặt phẳng (ABC) và (ABC)? A.
120
0
B.
60
0
C.
30
0
D.
45...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có diện tích đáy bằng a 2 3 (đvdt), diện tích tam giác A'BC bằng 2 a 2 (đvdt). Tính góc giữa hai mặt phẳng (A'BC) và (ABC)?
A. 120 0
B. 60 0
C. 30 0
D. 45 0
Cho lăng trụ tam giác đều ABC.ABC có diện tích đáy bằng
3
a
2
(đvdt), diện tích tam giác ABC bằng
2
a
2
(đvdt). Tính góc giữa hai mặt phẳng (ABC) và (ABC)? A.
120
o
B.
60
o
C....
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có diện tích đáy bằng 3 a 2 (đvdt), diện tích tam giác A'BC bằng 2 a 2 (đvdt). Tính góc giữa hai mặt phẳng (A'BC) và (ABC)?
A. 120 o
B. 60 o
C. 30 o
D. 45 o
Đáp án là C
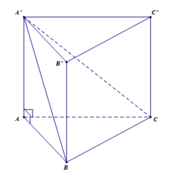
+) Ta có tam giác ABC là hình chiếu vuông góc của tam giác A'BC trên mặt phẳn (ABC)
+) Gọi φ là góc giữa (A'BC) và (ABC).
Ta có :
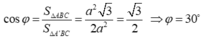
Đúng 0
Bình luận (0)
cho tam giác nhon ABC có S=1(đvdt).CM diện tích DEF=\(sin^2A-cos^2B-cos^2C\)
(biết AD,BE,CF là các đường cao)
Trước tiên ta chứng minh bài toán phụ: công thức tính diện tích tam giác ABC có góc A nhọn \(S_{\Delta ABC}=\frac{1}{2}AB.AC.\sin A\)
Giải: Kẻ đường cao BH thì \(BH=AB.\sin A\)do đó \(S_{\Delta ABC}=\frac{1}{2}AC.BH=\frac{1}{2}AC.AB.\sin A\)
Ta quay trở lại việc giải bài toán trên. (hình bạn tự vẽ nhé!)
Ta có \(S_{DEF}=S_{ABC}-S_{AEF}-S_{BDF}-S_{CDE}\)suy ra \(\frac{S_{DEF}}{S_{ABC}}=1-\frac{S_{AEF}}{S_{ABC}}-\frac{S_{BDF}}{S_{ABC}}-\frac{S_{CDE}}{S_{ABC}}.\)
Áp dụng bài toán phụ ta có \(\frac{S_{AEF}}{S_{ABC}}=\frac{\frac{1}{2}AE.AF.\sin A}{\frac{1}{2}AB.AC.\sin A}=\frac{AE.AF}{AB.AC}=\frac{AF}{AC}.\frac{AE}{AB}\)
Trong các tam giác vuông ACF và ABE có: \(\cos A=\frac{AF}{AC}\)và \(\cos A=\frac{AE}{AB}\)
Do đó \(\frac{S_{AEF}}{S_{ABC}}=\cos^2A\)tương tự \(\frac{S_{BDF}}{S_{ABC}}=\cos^2B\)và \(\frac{S_{CDE}}{S_{ABC}}=\cos^2C\)
Vậy \(\frac{S_{DEF}}{S_{ABC}}=\left(1-\cos^2A\right)-\cos^2B-\cos^2C=\sin^2A-\cos^2B-\cos^2C.\)
Hay \(S_{DEF}=\left(\sin^2A-\cos^2B-\cos^2C\right).S_{ABC}=\sin^2A-\cos^2B-\cos^2C\)(do \(S_{ABC}=1\)).
Đúng 0
Bình luận (0)
cho tam giác nhon ABC có S=1(đvdt).CM diện tích DEF=\(sin^2A-cos^2B-cos^2C\)
(biết AD,BE,CF là các đường cao)
1) Tìm giá trị nhỏ nhất của biểu thức:\(A=\frac{x^2+2x+9}{-2y-y^2+3}\)
2) Cho tam giác ABC vuông góc tại C.Đường cao CH và trung tuyến CM chia góc C thành 3 góc bằng nhau ( góc ACH= góc HCM = góc MCB).Biết diện tích của tam giác CHA =12(đvdt),tính diện tích của tam giác ABC ? (đvdt)
1) \(A=\frac{x^2+2x+9}{-2y-y^2+3}=\frac{\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\left(-y^2-2y+3\right)}{-y^2-2y+3}=\frac{\left(x+1\right)^2+2\left(y+1\right)^2}{-y^2-2y+3}+2\ge2\)Vậy Min A = 2 \(\Leftrightarrow\hept{\begin{cases}x=-1\\y=-1\end{cases}}\)
Đúng 0
Bình luận (0)
Cho hai hàm số y=-x+2 và y=x^2 có đồ thị lần lượt là (d) và (P).
Điểm A thuộc (P) có hoành độ –2; điểm B(0; –1), tìm điểm C thuộc trục hoành sao cho diện tích tam giác ABC bằng 4(đvdt).
Cho tam giác ABC có \(\hat B = {75^0};\hat C = {45^0}\) và \(a = BC = 12\;cm\).
a) Sử dụng công thức \(S = \frac{1}{2}ab.\sin C\) và định lí sin, hãy chứng minh diện tích của tam giác \(ABC\;\)cho bởi công thức \(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\)
b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.
a) Theo định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \to b = \frac{{a.\sin B}}{{\sin A}}\) thay vào \(S = \frac{1}{2}ab.\sin C\) ta có:
\(S = \frac{1}{2}ab.\sin C = \frac{1}{2}a.\frac{{a.\sin B}}{{\sin A}}.sin C = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\) (đpcm)
b) Ta có: \(\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat A = {180^0} - {75^0} - {45^0} = {60^0}\)
\(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}} = \frac{{{{12}^2}.\sin {{75}^0}.\sin {{45}^0}}}{{2.\sin {{60}^0}}} = \frac{{144.\frac{1}{2}.\left( {\cos {{30}^0} - \cos {{120}^0}} \right)}}{{2.\frac{{\sqrt 3 }}{2}\;}} = \frac{{72.(\frac{{\sqrt 3 }}{2}-\frac{{-1 }}{2}})}{{\sqrt 3 }} = 36+12\sqrt 3 \)
Đúng 0
Bình luận (0)















