Cho số thực a>0. Giả  sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) = 1 Tính tích phân  ∫ 0 1 1 1 + f ( x ) d x

A. I = a/2

B. I = a

C. I = 2a/3

D. I = a/3

Cho số thực a>0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) = 1 Tính tích phân  I = ∫ 0 a 1 1 + f ( x ) d x

A. a/3

B. a/2

C. a

D. 2a/3

Cho số thực a>0. Giả  sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân  I = ∫ 0 a 1 1 + f ( x ) d x

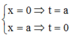
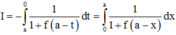
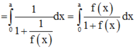
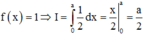
Cho số thực a > 0. Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f x . f a − x = 1.  Tính tích phân I = ∫ 0 a 1 1 + f x d x  

A.  I = a 3

B. I = a 2

C. I = a

D. I = 2 a 3

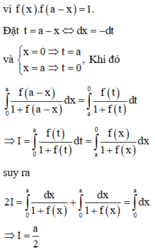
Cho hàm số y=f(x) đồng biến trên (0;+∞); y=f(x) liên tục, nhận giá trị dương trên (0;+∞) và thỏa mãn f 3 = 4 9  và f ' x 2 = ( x + 1 ) . f x . Tính f(8)

A. 49

B. 256

C.  1 16

D.  49 64

Cho các mệnh đề :

1) Hàm số y=f(x) có đạo hàm tại điểm x 0  thì nó liến tục tại  x 0 . 

2) Hàm số y=f(x) liên tục tại  x 0  thì nó có đạo hàm tại điểm  x 0 .

3) Hàm số y=f(x) liên tục trên đoạn [a;b] và f(a).f(b)<0 thì phương trình f(x) có ít nhất một nghiệm trên khoảng (a;b).

4) Hàm số y=f(x) xác định trên đoạn [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Số mệnh đề đúng là:

A. 2

B. 4

C. 3

D. 1

Cho hàm số f(x) luôn dương và có đạo hàm liên tục trên đoạn [1;4]. Biết rằng f ' ( x ) = e x f ( x ) , ∀ x∈ [1;4] và f(1)=1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f' (x)=1, trục hoành và hai đường thẳng x=1,x=4.  

A.  e e 2 + 1 .

B.  e 2 e 2 + 1 .

C.  e 2 e 2 + 2 .

D.  e e 2 + 2 .

Cho hàm số y = f(x) liên tục, luôn dương trên [0;3] và thỏa mãn I = ∫ 0 3 f x d x = 4 . Khi đó giá trị của tích phân K = ∫ 0 3 e 1 + ln f x + 4 d x là:

A. 3e+14

B. 14e + 3

C. 4 + 12e

D. 12 + 4e