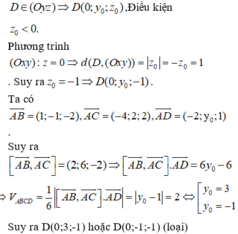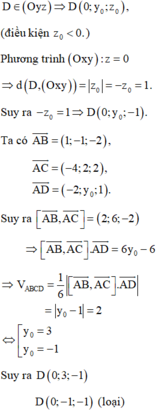Trong mặt phẳng Oxy cho HCN ABCD có điểm B (1;3) và diện tích là 30goij E là điểm nằm trên cạnh BC sao cho EC =2EB điểm H(5/2;5/2) là hình chiếu vuông góc trên DE Biết C có tung độ âm , Tìm tọa độ các hình chữ nhật

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho hcn ABCD tâm O, AB:x-y+5=. Trung điểm M của BC thuộc đt x+3y-6=0. Xác định tọa độ các đỉnh hcn ABCD.
Phương trình đường thẳng qua O và song song AB có dạng: \(x-y=0\)
\(\Rightarrow\) Tọa độ M là nghiệm của hệ: \(\left\{{}\begin{matrix}x+3y-6=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow M\left(\frac{3}{2};\frac{3}{2}\right)\)
Phương trình đường thẳng BC qua M, nhận \(\left(1;1\right)\) là 1 vtpt có dạng:
\(1\left(x-\frac{3}{2}\right)+1\left(y-\frac{3}{2}\right)=0\Leftrightarrow x+y-3=0\)
Tọa độ B là nghiệm của hệ: \(\left\{{}\begin{matrix}x-y+5=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow B\)
M là trung điểm BC \(\Rightarrow\) tọa độ C
O là trung điểm AC \(\Rightarrow\) tọa độ A
O là trung điểm BD \(\Rightarrow\) tọa độ D
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.
A.D(0; -1)
B. D( 2; -3)
C. D( 2; -3); D(0; 1)
D. D( -2; -3)
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-1;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là: A. D(0;-3;-1) B. D(0;1;-1) C. D(0;2;-1) D. D(0;3;-1)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-1;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là:
A. D(0;-3;-1)
B. D(0;1;-1)
C. D(0;2;-1)
D. D(0;3;-1)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-2;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương và cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là: A.
D
0
;
−
3
;
−
1
B.
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2;0;-2), B(3;-2;-4), C(-2;2;0). Điểm D trong mặt phẳng (Oyz) có tung độ dương và cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt phẳng (Oxy) bằng 1 có thể là:
A. D 0 ; − 3 ; − 1
B. D 0 ; 1 ; − 1
C. D 0 ; 2 ; − 1
D. D 0 ; 3 ; − 1
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông
Trong mặt phẳng tọa độ Oxy, cho 3 điểm có A(-3;-2); B(3;6); C(11;0). Tìm tọa độ điểm D để tứ giác ABCD là hình vuông
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. D( -8; 5).
B. D( 5; 8).
C. D( 8; 5).
D. D( 8; -5).
Chọn D.
Ta có: tứ giác ABCD là hình bình hành khi

Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A.D( -8; 5)
B. D( 5; 8)
C.D( 8; 5)
D.D( 8; -5) .
Ta có: tứ giác ABCD là hình bình hành khi
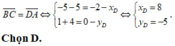
Đúng 0
Bình luận (0)
Trong mặt phẳng oxy cho 3 điểm A(-5;2) B(4:-3) C(6:1) tìm tọa độ D để tứ giác abcd là hình bình hành
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(9;-5\right)\\\overrightarrow{CD}=\left(6-x;1-y\right)\end{matrix}\right.\)
ABCD là hình bình hành khi \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}6-x=9\\1-y=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-3\\y=6\end{matrix}\right.\)
\(\Rightarrow D\left(-3;6\right)\)
Đúng 0
Bình luận (0)