Trong không gian với hệ tọa độ Oxyz, cho điểm H(2; –1;2) là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (P). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) có phương trình – y + z = 0 là:
A. 90 0 .
B. 60 0 .
C. 45 0 .
D. 30 0 .
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(2;0;4)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(0;-1;0).
Đáp án C
Do chiếu xuống (Oxy) nên z=0 và x,y giữ nguyên.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(0;-1;0)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(2;0;4).
Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;-13). Gọi H là hình chiếu vuông góc của M trên mặt phẳng (Oxz) Tọa độ điểm H là:
A. H(1;2;-13)
B. H(1;0;0)
C. H(1;-2;0)
D. H(1;0;-13)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A - 1 ; 0 ; 1 , B 1 ; 1 ; - 1 , C 5 ; 0 ; - 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH là thành hình thang cân với hai đáy AB, CH.
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Chọn C.
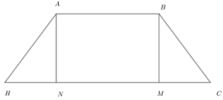
Phương pháp: Sử dụng các véc tơ bằng nhau.

Giả sử M,N lần lượt là hình chiếu của A, B lên CH.
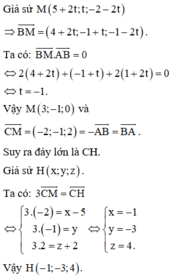
Trong không gian với hệ trục tọa độ Oxyz cho điểm M 2 ; 1 ; 4 . Điểm H thuộc đường thẳng Δ : x = 1 + t y = 2 + t z = 1 + 2 t t ∈ ℝ sao cho đoạn MH ngắn nhất có tọa độ là:
A. 2 ; 3 ; 2
B. 3 ; 2 ; 3
C. 3 ; 3 ; 2
D. 2 ; 3 ; 3
Đáp án D
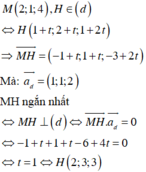
Bình luận: Nhận thấy ở các đáp án chỉ có điểm
H 2 ; 3 ; 3 ∈ d .
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A 4 ; 1 ; − 2 . Tọa độ điểm đối xứng với A qua mặt phẳng O x z là
A. A ' 4 ; − 1 ; 2
B. A ' − 4 ; − 1 ; 2
C. A ' 4 ; − 1 ; − 2
D. A ' 4 ; 1 ; 2
Đáp án C.
Gọi điểm H là hình chiếu của A 4 ; 1 ; − 2 trên mặt phẳng O x z , khi đó H 4 ; 0 ; − 2 .
Điểm A' đối xứng với A 4 ; 1 ; − 2 qua mặt phẳng O x z nên H 4 ; 0 ; − 2 là trung điểm AA' . Khi đó A ' 2 x H − x A ; 2 y H − y A ; 2 z H − z A → A ' 4 ; − 1 ; − 2
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 3 ; 0 ; − 2 và B 1 ; 4 ; 2 . Tọa độ của vectơ A B → là
A. − 1 ; 2 ; 2 .
B. − 2 ; 4 ; 4 .
C. 2 ; 2 ; 0 .
D. 4 ; 4 ; 0 .
Trong không gian với hệ tọa độ Oxyz, cho các điểm A − 1 ; 0 ; 1 , B 1 ; 1 ; − 1 , C 5 ; 0 ; − 2 . Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH
A. H(3;-1;0)
B. H(7;1;-4)
C. H(-1;-3;4)
D. H(1;-2;2)
Trong không gian với hệ tọa độ Oxyz, cho điểm I (1;2;3) và mặt phẳng(P): 2x-2y-z-4=0. Mặt cầu tâm I tiếp xúc với (P) tại điểm H. Tìm tọa độ H.
A. H(-1;4;4)
B. H(-3;0;-2)
C. H(3;0,2)
D. H(1;-1;0)
Đáp án C
Mặt cầu tâm I tiếp xúc với (P) tại H ⇒ I H ⊥ ( P )
nên IH nhận vecto pháp tuyến của (P) làm vecto chỉ phương
⇒
phương trình của IH:
x
=
1
+
2
t
y
=
2
-
2
t
z
=
3
-
1
⇒
H
(
1
+
2
t
;
2
-
2
t
;
3
-
t
)
∈
(
P
)
⇒ 2(1+2t)-2(2-2t)-(3-t)-4=0 ⇔ t=1 ⇒ H(3;0;2)
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;2;3) và mặt phẳng P : 2 x − 2 y − z − 4 = 0 . Mặt cầu tâm I tiếp xúc với (P) tại điểm H. Tìm tọa độ H.
A. H − 1 ; 4 ; 4 .
B. H − 3 ; 0 ; − 2 .
C. H 3 ; 0 ; 2 .
D. H 1 ; − 1 ; 0 .
Đáp án C
Vectơ pháp tuyến của mặt phẳng (P) là n → = 2 ; − 2 ; − 1
Gọi u → là vectơ chỉ phương của đường thẳng IH
Vì IH ⊥ P nên u → = n → = 2 ; − 2 ; − 1
Phương trình đường thẳng IH qua I(1;2;3) và có vectơ chỉ phương u → = 2 ; − 2 ; − 1 là x = 1 + 2 t y = 2 − 2 t z = 3 − t
Tọa độ của H ∈ IH là H 1 + 2 t ; 2 − 2 t ; 3 − t
Mặt cầu tâm I tiếp xúc với (P) tại điểm H nên H ∈ P
Khi đó 2 1 + 2 t − 2 2 − 2 t − 3 − t − 4 = 0
⇒ t = 1 ⇒ H 3 ; 0 ; 2