Cho \(y=f\left(x\right)=2x^2-4x-1\) Có bao nhiêu giá trị nguyên \(m\in\left[-10;10\right]\) để phương trình \(f^2\left(\left|x\right|\right)+\left(m-1\right)f\left(\left|x\right|\right)-m=0\) có 4 nghiệm phân biệt

Những câu hỏi liên quan
Cho hàm số \(y=f\left(x\right)\) có đạo hàm \(f'\left(x\right)=\left(x-2\right)^2\left(x-1\right)\left(x^2-2\left(m+1\right)x+m^2-1\right)\) , \(\forall x\in R\) . Có bao nhiêu giá trị nguyên của m để hàm số \(g\left(x\right)=f\left(\left|x\right|\right)\) có 5 điểm cực trị ?
đi từ hướng làm để ra được bài toán:
Ta thấy muốn f(|x|) có 5 điểm cực trị thì f'(x) phải có 2 điểm cực trị dương
giải f'(x)=0 \(\left\{{}\begin{matrix}x=1\\x^2-2\left(m+1\right)x+m^2-1=0\left(2\right)\end{matrix}\right.\) phương trình (2) phải có 2 nghiệm phân biệt trái dấu nhau
Ta có: \(\Delta>0\Leftrightarrow m>-1\)
Theo yêu cầu bài toán: \(m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m ∈ (-10; 10) để hàm số y = f(x) = \(\left|3x^4-4x^3-6mx^2+12mx\right|\) có đúng 3 điểm cực trị
\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
Đúng 0
Bình luận (3)
Cho hàm đa thức yleft[fleft(x^2+2xright)right] có đồ thị cắt trục Ox tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số m2022min Z để hàm số gleft(xright)fleft(x^2-2left|x-1right|-2x+mright) có 9 điểm cực trị?Giúp mình với ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hàm đa thức \(y=\left[f\left(x^2+2x\right)\right]'\) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m=2022m\in Z\) để hàm số \(g\left(x\right)=f\left(x^2-2\left|x-1\right|-2x+m\right)\) có 9 điểm cực trị?
Giúp mình với ạ, mình cảm ơn nhiều♥
đề bài thiếu, ko giải được, cái nghiệm -1 có thể của f(u) hoặc của u'
Đúng 0
Bình luận (1)
Cho hàm số bậc ba yfleft(xright) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số minleft[0;20right] để hàm số gleft(xright)left|f^2left(xright)-2fleft(xright)-mright| có 9 điểm cực trị?A. 8 B. 9 C. 10 D. 11Giải chi tiết cho mình bài này với ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho hàm số bậc ba \(y=f\left(x\right)\) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\in\left[0;20\right]\) để hàm số \(g\left(x\right)=\left|f^2\left(x\right)-2f\left(x\right)-m\right|\) có 9 điểm cực trị?
A. 8 B. 9 C. 10 D. 11
Giải chi tiết cho mình bài này với ạ, mình cảm ơn nhiều♥

Đặt \(h\left(x\right)=f^2\left(x\right)-2f\left(x\right)-m\Rightarrow h'\left(x\right)=2f'\left(x\right)\left[f\left(x\right)-1\right]\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f\left(x\right)=1\end{matrix}\right.\)
Từ đồ thị ta thấy \(f'\left(x\right)=0\) có 2 nghiệm (do \(f\left(x\right)\) có 2 cực trị) và \(y=1\) cắt \(y=f\left(x\right)\) tại 3 điểm
\(\Rightarrow h'\left(x\right)=0\) có 5 nghiệm
\(\Rightarrow\) Hàm \(g\left(x\right)\) có 9 cực trị khi \(f^2\left(x\right)-2f\left(x\right)-m=0\) có 4 nghiệm không trùng với nghiệm của \(h'\left(x\right)=0\)
TH1: \(m=0\Rightarrow f^2\left(x\right)-2f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}f\left(x\right)=0\\f\left(x\right)=2\end{matrix}\right.\)
\(f\left(x\right)=0\) có 2 nghiệm, trong đó 1 nghiệm trùng với \(f'\left(x\right)=0\) nên chỉ tính 1 nghiệm, \(f\left(x\right)=2\) có 3 nghiệm \(\Rightarrow f^2\left(x\right)-2f\left(x\right)=0\) có 4 nghiệm ko trùng \(h'\left(x\right)=0\) (thỏa mãn)
TH2: \(m>0\), đặt \(k=f\left(x\right)\Rightarrow k^2-2k-m=0\) (1) luôn có 2 nghiệm pb trái dấu \(k_1< 0< k_2\) do \(c=-m< 0\)
Từ đồ thị ta thấy \(f\left(x\right)=k_1\) luôn có đúng 1 nghiệm
Do đó, \(f\left(x\right)=k_2\) phải có 3 nghiệm phân biệt đồng thời \(k_2\ne1\) \(\Rightarrow\left\{{}\begin{matrix}0< k_2< 4\\k_2\ne1\end{matrix}\right.\)
(\(k_2\) là nghiệm dương của (1) nên \(k_2=1+\sqrt{m+1}\))
\(\Rightarrow\left\{{}\begin{matrix}0< 1+\sqrt{m+1}< 4\\1+\sqrt{m+1}\ne1\end{matrix}\right.\) \(\Rightarrow m< 8\Rightarrow m=\left\{1;2;3;4;5;6;7\right\}\)
Kết hợp lại ta được \(m=\left\{0;1;...;7\right\}\) có 8 giá trị nguyên của m thỏa mãn
Đúng 1
Bình luận (0)
Cho hàm số fleft(xright)left|x^2-2x+mright| với minleft[-2018;2018right]. Gọi M là giá trị nhỏ nhất của hàm số fleft(x+dfrac{1}{x}right) trên tập Rbackslashleft{0right}. Số giá trị m nguyên để Mge2 là bao nhiêu?
Đọc tiếp
Cho hàm số \(f\left(x\right)=\left|x^2-2x+m\right|\) với \(m\in\left[-2018;2018\right]\). Gọi \(M\) là giá trị nhỏ nhất của hàm số \(f\left(x+\dfrac{1}{x}\right)\) trên tập \(R\backslash\left\{0\right\}\). Số giá trị \(m\) nguyên để \(M\ge2\) là bao nhiêu?
Cho hàm số fleft(xright) xác định trên R, có đạo hàm fleft(xright)left(x^2-4right)left(x-5right)forall xin R và fleft(1right)0. Có bao nhiêu giá trị nguyên của tham số m để hàm số gleft(xright)left|fleft(x^2+1right)-mright| có nhiều điểm cực trị nhất?A.7 B. 8 C. 5 D. 6
Đọc tiếp
Cho hàm số \(f\left(x\right)\) xác định trên \(R\), có đạo hàm \(f'\left(x\right)=\left(x^2-4\right)\left(x-5\right)\forall x\in R\) và \(f\left(1\right)=0\). Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g\left(x\right)=\left|f\left(x^2+1\right)-m\right|\) có nhiều điểm cực trị nhất?
A.7 B. 8 C. 5 D. 6

\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:

Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m
Đúng 1
Bình luận (2)
a) Cho hàm số yx^2+2x+3+left|x-a+1right| có bao nhiêu giá trị nguyên của tham số ainleft[-10;10right] sao cho giá trị nhỏ nhất của hàm số lớn hơn 2b) Tìm tất cả các giá trị của tham số m để hệ bất pt left{{}begin{matrix}x^2-2x-3le0x^2-2mx+m^2-9ge0end{matrix}right. có nghiệmc) Gọi (x;y) là nghiệm của hệ bất pt left{{}begin{matrix}x-2y-2le04x-3y+12ge0x+3y+3ge02x+y-4le0end{matrix}right.. Tìm giá trị lớn nhất của biểu thức F4x+5y-6
Đọc tiếp
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số \(m\in[-2020;2020]\) để bất phương trình \(\left|4x-2m-\dfrac{1}{2}\right|>-x^2+2x+\dfrac{1}{2}-m\) luôn đúng với mọi \(x\).
Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\), có bao nhiêu giá trị nguyên của tham số a \(\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2












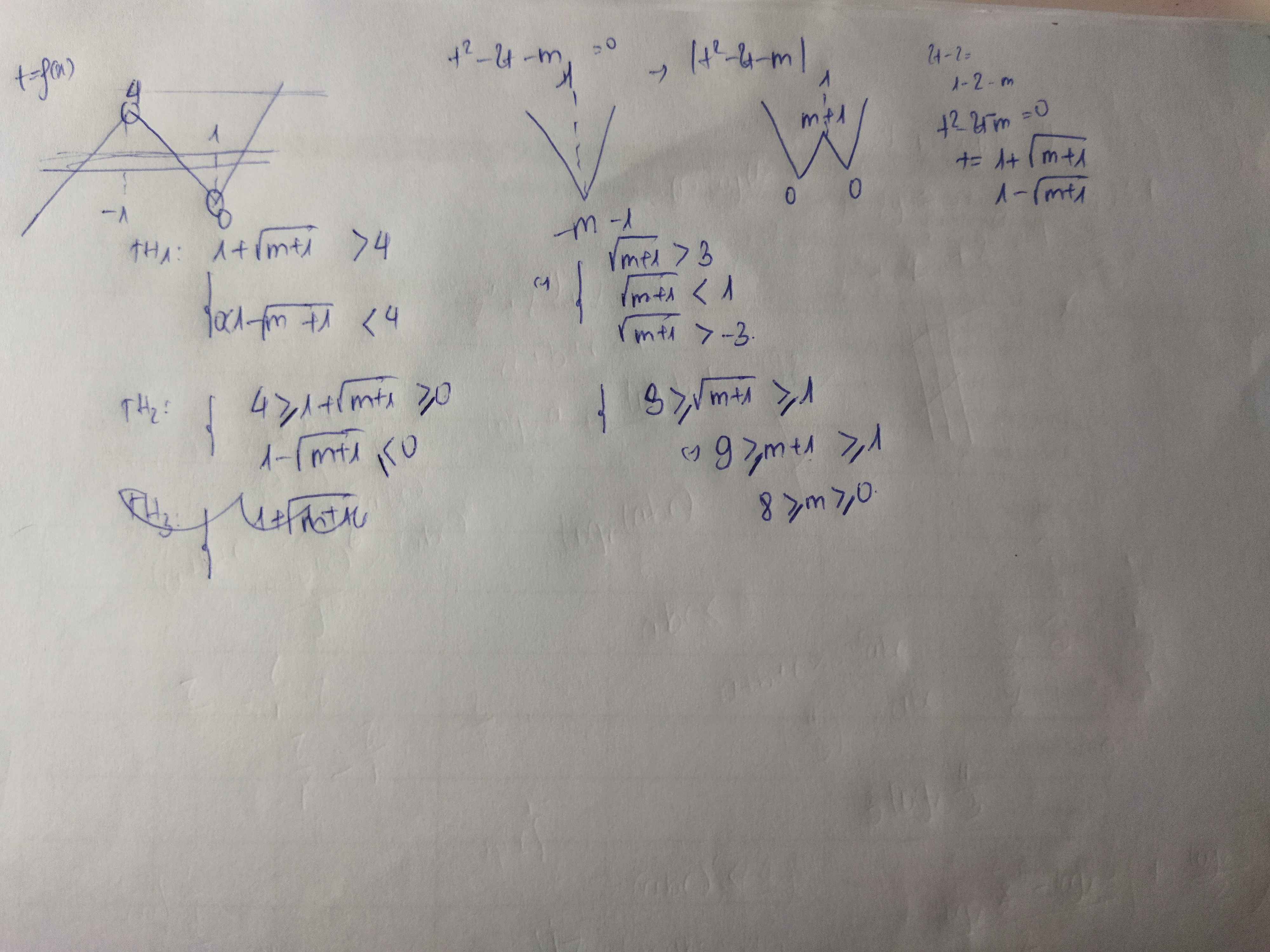 9 đko nhỉ
9 đko nhỉ



