cho \(\Delta ABC\) cân A nọi tiếp đường tròn \(\left(O;10\right)\) biết AH =BC tính SABC

Những câu hỏi liên quan
Cho \(\Delta ABC\) cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D.
1) Vì sao AD là đường kính của đường tròn (O)
2) Tính \(\widehat{ACD}\)
3) Cho BC = 24cm; AC = 20cm. Tính đường cao AH và bán kính đường tròn (O)
1: ΔABC cân tại A
=>AB=AC
mà OB=OC
nên AO là trung trực của BC
=>AD là đường kính của (O)
2: Xét (O) có
góc ACD là góc nội tiếp chắn nửa đường tròn
=>góc ACD=90 độ
3: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=12cm
AH=căn AB^2-AH^2=16cm
ΔACD vuông tại C có CH là đường cao
nên AC^2=AH*AD
=>AD=20^2/16=25cm
=>R=12,5cm
Đúng 1
Bình luận (0)
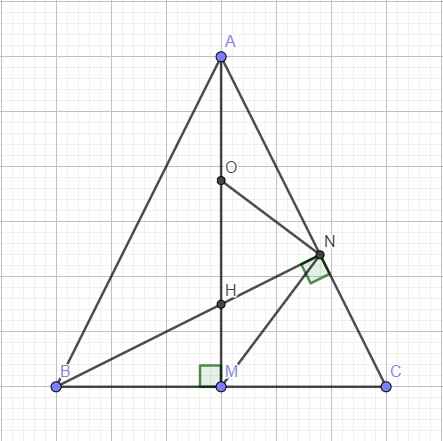
Cho \(\Delta ABC\) cân tại A, các đường cao AM và BN cắt nhau tại H. Chứng minh rằng MN là tiếp tuyến của đường tròn tâm O đường kính AH.
Gọi O là trung điểm AH, tam giác AHN vuông tại N nên N thuộc đường tròn đường kính AH
Do ABC cân tại A \(\Rightarrow\) AM là đường cao đồng thời là trung tuyến
\(\Rightarrow\) M là trung điểm BC
Trong tam giác vuông NBC, NM là trung tuyến ứng với cạnh huyền
\(\Rightarrow MN=MB=\dfrac{1}{2}BC\Rightarrow\Delta MNB\) cân tại M
\(\Rightarrow\widehat{MNB}=\widehat{MBN}\) (1)
Tương tự, trong tam giác vuông ANH, ta có: \(ON=OH=\dfrac{1}{2}AH\Rightarrow\widehat{ONH}=\widehat{OHN}\)
Mà \(\widehat{OHN}=\widehat{MHB}\) (đối đỉnh) \(\Rightarrow\widehat{ONH}=\widehat{MHB}\) (2)
Lại có tam giác HBM vuông tại M \(\Rightarrow\widehat{MHB}+\widehat{MBN}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{ONH}+\widehat{MNB}=90^0\) hay \(MN\perp ON\)
\(\Rightarrow MN\) là tiếp tuyến của đường tròn đường kính AH
Đúng 3
Bình luận (0)
Cho \(\Delta ABC\)cân ở A, nội tiếp đường tròn (O). Dọi D là 1 điểm trên cạnh BC, tia AD cắt đường tròn ở E. Chứng minh:
a) \(AB^2=AD.AE\)
b) AB là tiếp tuyến của đường tròn ngoại tiếp \(\Delta BED\)
cho tam giác ABC nhọn (ABAC) nội tiếp đường tròn tâm O . Hai đường cao BE ,CF của tam giác ABC cắt hau tại HA. chứng minh các từ giác AFHE và BCEF nọi tiếp được , xác định tâm của đường tròn ngoại tiếpB/ Đường thẳng EF cắt đường thẳng BC tại M , đoạn thẳng AM cắt đường tròn O tại N , chứng minh tứ giác AEFN nội tiếpC. kẻ đường kính AK của đường tròn O . chứng minh ba điểm N,H,K thẳng hàngthank :333
Đọc tiếp
cho tam giác ABC nhọn (AB<AC) nội tiếp đường tròn tâm O . Hai đường cao BE ,CF của tam giác ABC cắt hau tại H
A. chứng minh các từ giác AFHE và BCEF nọi tiếp được , xác định tâm của đường tròn ngoại tiếp
B/ Đường thẳng EF cắt đường thẳng BC tại M , đoạn thẳng AM cắt đường tròn O tại N , chứng minh tứ giác AEFN nội tiếp
C. kẻ đường kính AK của đường tròn O . chứng minh ba điểm N,H,K thẳng hàng
thank :333
a) Ta có: \(\angle AFH+\angle AEH=90+90=180\Rightarrow AEHF\) nội tiếp
Gọi D là trung điểm AH
Vì \(\Delta AEH\) vuông tại E có D là trung điểm AH \(\Rightarrow DE=DA=DH\)
Tương tự \(\Rightarrow DF=DA=DH\Rightarrow DE=DF=DA=DH\)
\(\Rightarrow D\) là tâm (AEHF)
Tương tự,ta chứng minh BCEF nội tiếp đường tròn có tâm là BC
b) Xét \(\Delta MFB\) và \(\Delta MCE:\) Ta có: \(\left\{{}\begin{matrix}\angle EMCchung\\\angle MFB=\angle MCE\end{matrix}\right.\)
\(\Rightarrow\Delta MFB\sim\Delta MCE\left(g-g\right)\Rightarrow\dfrac{MF}{MC}=\dfrac{MB}{ME}\Rightarrow ME.MF=MB.MC\)
Xét \(\Delta MNB\) và \(\Delta MCA:\) Ta có: \(\left\{{}\begin{matrix}\angle AMCchung\\\angle MNB=\angle MCA\end{matrix}\right.\)
\(\Rightarrow\Delta MNB\sim\Delta MCA\left(g-g\right)\Rightarrow\dfrac{MN}{MC}=\dfrac{MB}{MA}\Rightarrow MN.MA=MB.MC\)
\(\Rightarrow MN.MA=ME.MF\Rightarrow\dfrac{MN}{ME}=\dfrac{MF}{MA}\)
Xét \(\Delta MNF\) và \(\Delta MEA:\) Ta có: \(\left\{{}\begin{matrix}\angle AMEchung\\\dfrac{MN}{ME}=\dfrac{MF}{MA}\end{matrix}\right.\)
\(\Rightarrow\Delta MNF\sim\Delta MEA\left(c-g-c\right)\Rightarrow\angle MNF=\angle MEA\Rightarrow ANFE\) nội tiếp
c) ANFE nội tiếp mà AEHF nội tiếp \(\Rightarrow A,E,H,F,N\) cùng thuộc 1 đường tròn
\(\Rightarrow\angle ANH=\angle AFH=90\Rightarrow NH\bot AN\)
Vì AK là đường kính \(\Rightarrow\angle ANK=90\Rightarrow NK\bot AN\)
\(\Rightarrow N,H,K\) thẳng hàng
Đúng 1
Bình luận (1)
Cho đường tròn (O) và một điểm A nằm ngoài dường tron (O). Qua A vẽ các tiếp tuyến AB, AC với đường tron (O) (B,C là các tiếp điểm), AO cắt BC tại D.a) Chứng minh Delta ABCcân tại A và AO là đường trung trực của BCb) Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh: Delta AGOapproxDelta HDO(hai tam giác đồng dạng)c) Chứng minh EH là tiếp tuyến của đường tròn (O)
Đọc tiếp
Cho đường tròn (O) và một điểm A nằm ngoài dường tron (O). Qua A vẽ các tiếp tuyến AB, AC với đường tron (O) (B,C là các tiếp điểm), AO cắt BC tại D.
a) Chứng minh \(\Delta ABC\)cân tại A và AO là đường trung trực của BC
b) Vẽ đường kính BE, AE cắt đường tròn (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh: \(\Delta AGO\approx\Delta HDO\)(hai tam giác đồng dạng)
c) Chứng minh EH là tiếp tuyến của đường tròn (O)
Các bước giải Thương của hai số được tính. Thương được nhân với 100100100để tìm tỉ số phần trăm. Lời giải chi tiết Thương của 36,9636 comma 9636,96và 424242được tính: 36,9642=0,88the fraction with numerator 36 comma 96 and denominator 42 end-fraction equals 0 comma 8836,9642=0,88. Tỉ số phần trăm được tính bằng cách nhân thương với 100100100: 0,88×100=88%0 comma 88 cross 100 equals 88 %0,88×100=88%. Đáp án cuối cùng Tỉ số phần trăm của 36,9636 comma 9636,96và 424242là 88%88 %88%.
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) nhọn và nội tiếp đường tròn(O,R).Các đường cao AM,BN của \(\Delta ABC\) cắt nhau tại H(\(M\in BC,N\in AC\)).Tia AM cắt cung nhỏ BC của đường tròn(O,R) tại D.Kẻ đường kính AE của đường tròn(O,R)
a)CMR:BC//DE
b)\(CMR:S_{ABC}=\dfrac{AB.BC.CA}{4R}\)
cho tam giác ABC nhọn nội tiếp đường tròn (O) ,có 2 đường cao BE và CF.Hai tiếp tuyến của O tại B ,C cắt nhau tại K.Đường thẳng AK cắt đường tròn (O) tại D
a) chứng minh BFEC nội tiếp
b) chứng minh \(\Delta\)KBD \(\sim\)\(\Delta\)KAB và AB.CD=AC.BD
c) chứng minh AK đi qua trung điểm EF
Cho \(\Delta ABC\) ngoại tiếp đường tròn (I). Một đường tròn qua B, C cắt BI, CI lần tại P, Q sao cho \(BP.CQ=PI.QI\). Chứng minh rằng:
a) \(\left(PQI\right)\) tiếp xúc với \(\left(ABC\right)\) (gọi tiếp điểm là T)
b) IT đi qua trung điểm của đoạn PQ.
cho \(\Delta ABC\) cân nội tiếp đường tròn (O;R) ,\(\widehat{A}< 90^0\) . Gọi H,I lần lượt là trung điểm của AB và AC . Nối OH,OI cắt các cung nhỏ AB,AC lần lượt tại M,N
a) c/m OA\(\perp\)MN
b) \(\Delta ABC\) phải thêm điều kiện gì để OMAN là hình thoi