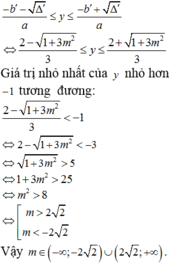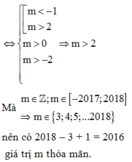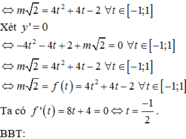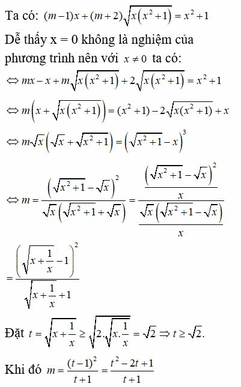Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( -10; 10) sao cho đồ thị hám số y = \(^{x^3-2mx^2+\left(2m+6\right)x}\) có 2 điểm cực trị nằm về 2 phía khác nhau của trục hoành

Những câu hỏi liên quan
Cho hàm số
y
m
.
sin
x
+
1
cos
x
+
2
. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng
-
10
;
10
để giá trị nhỏ nhất của y nhỏ hơn -1. A. 14 B. 13 C. 12 D. 15
Đọc tiếp
Cho hàm số y = m . sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng - 10 ; 10 để giá trị nhỏ nhất của y nhỏ hơn -1.
A. 14
B. 13
C. 12
D. 15
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
+
2
x
+
m
đồng biến trên khoảng
-
∞
;
-
10
? A. 7. B. Vô số. C. 9. D. 8.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 2 x + m đồng biến trên khoảng - ∞ ; - 10 ?
A. 7.
B. Vô số.
C. 9.
D. 8.

Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số
y
1
3
x
3
-
m
x
2
+
(
m
+
2
)
x
có hai điểm cực trị nằm trong khoảng
0...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y
1
3
x
3
-
m
x
2
+
(
m
+
2
)
x
có hai điểm cực trị nằm trong khoảng
0
;
+
∞
. A. 2015 B. 2016 C. 2018 D. 4035
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
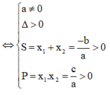
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
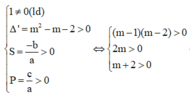
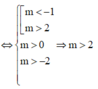
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-6;5) sao cho hàm số
f
x
-
sin
2
x
+
4
cos
x
+
m
x
2
không có cực trị trên đoạn
-
π
2
;
π
2
? A. 5 B. 4 C. 3 D. 2
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-6;5) sao cho hàm số f x = - sin 2 x + 4 cos x + m x 2 không có cực trị trên đoạn - π 2 ; π 2 ?
A. 5
B. 4
C. 3
D. 2
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng
-
1000
;
1000
để hàm số
y
2
x
3
-
3
2
m
+
1
x
2
+
6
m
m
+
1...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng - 1000 ; 1000 để hàm số y = 2 x 3 - 3 2 m + 1 x 2 + 6 m m + 1 x + 1 đồng biến trên khoảng 2 ; + ∞ ?
A. 999
B. 1001
C. 1998
D. 998
Ta có:
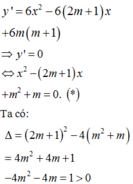
⇒ * luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2 với mọi m.
Áp dụng hệ thức Vi-ét ta có:
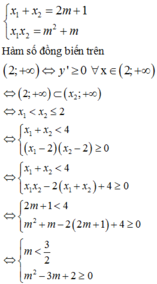
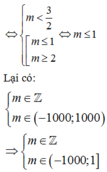
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.
Chọn B.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng
-
2019
;
2019
để hàm số
y
sin
3
x
-
3
cos
2
x
+
m
sin
x
-
1
đồng biến trên đoạn . A. 2020. B. 2019. C. 2028. D. 2018.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng - 2019 ; 2019 để hàm số y = sin 3 x - 3 cos 2 x + m sin x - 1 đồng biến trên đoạn .
A. 2020.
B. 2019.
C. 2028.
D. 2018.
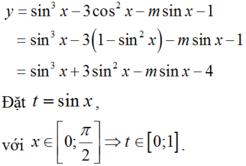
Bài toán trở thành tìm m để hàm số y = t 3 + 3 t 2 - m t - 4 đồng biến trên 0 ; 1 .
TXĐ: D = R .
Ta có y ' = 3 t 2 + 6 t - m
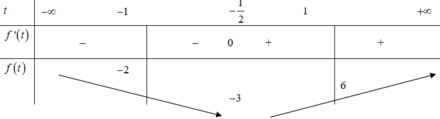
Để hàm số đồng biến trên 0 ; 1
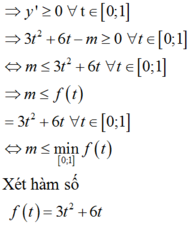
ta có TXĐ:
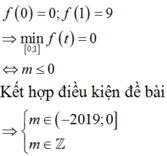
Có 2019 giá trị của m thỏa mãn.
Chọn B.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-6;5) sao cho hàm số
f
(
x
)
-
sin
2
x
+
4
cos
x
+
m
x
2
không có cực trị trên đoạn
-
π
2
;
π
2
? A. 5 B. 4 C. 3 D...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-6;5) sao cho hàm số f ( x ) = - sin 2 x + 4 cos x + m x 2 không có cực trị trên đoạn - π 2 ; π 2 ?
A. 5
B. 4
C. 3
D. 2
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-1;7) để phương trình
(
m
-
1
)
x
+
(
m
+
2
)
x
(
x
2
+
1
)
x
2
+
1
có nghiệm? A. 6 B. 7 C. 1 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-1;7) để phương trình ( m - 1 ) x + ( m + 2 ) x ( x 2 + 1 ) = x 2 + 1 có nghiệm?
A. 6
B. 7
C. 1
D. 5
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số
y
3
-
x
-
3
3
-
x
-
m
nghịch biến trên khoảng (-1;1). A. 4 B. 3 C. 2 D. 0
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số y = 3 - x - 3 3 - x - m nghịch biến trên khoảng (-1;1).
A. 4
B. 3
C. 2
D. 0
Chọn B
Phương pháp: Sử dụng đạo hàm của hàm hợp để tính đạo hàm.

Đúng 0
Bình luận (0)