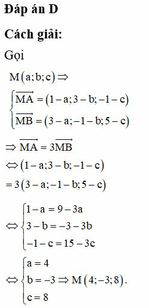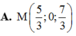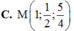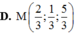18. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm \(A\left(3;-4;0\right)\) , \(B\left(0;2;4\right)\) , \(C\left(4;2;1\right)\) . Tìm tọa độ điểm D thuộc trục Ox sao cho AD = BC
A. \(\left[{}\begin{matrix}D\left(0;0;0\right)\\D\left(6;0;0\right)\end{matrix}\right.\)
B. \(D\left(0;-6;0\right)\)
C. \(\left[{}\begin{matrix}D\left(0;0;0\right)\\D\left(-6;0;0\right)\end{matrix}\right.\)
D. \(D\left(6;0;0\right)\)
11. Trong không gian với hệ tọa Oxyz, mặt cầu \(\left(S\right):\) \(x^2+y^2+z^2-2x+4y-4=0\) cắt mp \(\left(P\right):\) \(x+y-z+4=0\) theo giao tuyến đường tròn \(\left(C\right)\) . Tính diện tích S của đường tròn \(\left(C\right)\)
A. \(S=\frac{2\pi\sqrt{78}}{3}\)
B. \(S=2\pi\sqrt{6}\)
C. \(S=6\pi\)
D. \(S=\frac{26\pi}{3}\)
14. Trong không gian Oxyz, mặt cầu tâm \(I\left(1;2;-1\right)\) cắt mp \(\left(P\right):\) \(x-2y-2z-8=0\) theo một đường tròn có bán kính bằng 4 có pt là
A. \(\left(x+1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=5\)
B. \(\left(x-1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=9\)
C. \(\left(x-1\right)^2+\left(y-2\right)^2+\left(z+1\right)^2=25\)
15. Trong không gian với hệ tọa độ Oxyz, cho 3 điểm \(A\left(2;-1;3\right)\) , \(B\left(4;0;1\right)\) , \(C\left(-10;5;3\right)\) Vecto nào dưới đây là VTPT của mp \(\left(ABC\right)\)
A. \(\overrightarrow{n_1}\left(1;2;0\right)\)
B. \(\overrightarrow{n_2}\left(1;2;2\right)\)
C. \(\overrightarrow{n_3}\left(1;8;2\right)\)
D. \(\overrightarrow{n_4}\left(1;-2;2\right)\)
D. \(\left(x+1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=3\)