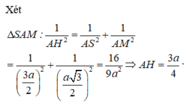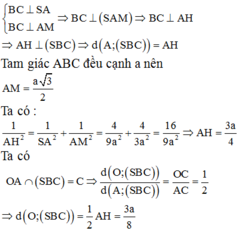cho hình thoi ABCD có A(2;1) và trung điểm I = AC\(\cap\) BC có tọa độ I(-2;3) tìm tọa độ B ;C ;D

Những câu hỏi liên quan
Cho hình thoi abcd có góc a=30°đường cao bh=1,5cm. Tính chu vi hình thoi abcd
\(AB=\dfrac{BH}{\sin A}=\dfrac{1,5}{\sin30^0}=3\left(cm\right)\)
Do đó \(P_{ABCD}=4AB=12\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho hình thoi ABCD có góc A=60 độ, AB=10cm. Tính diện tích hình thoi ABCD.
Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
Cho hình thoi ABCD có BD = 2a và AC = 8a. Tính a biết diện tích của hình thoi ABCD là 32cm2 .
Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)
\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)
\(\Rightarrow8a^2=32\)
\(\Rightarrow a^2=4\)
\(\Rightarrow a=2\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thoi ABCD có 2 đường chéo AC bằng 30cm ; DB bang 40 cm. Chu vi hình thoi là 100 cm. a. Tinh chieu cao hinh thoi. b.
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
⏜
60
°
,
S
A
⊥
A
B
C
D
,
S
A
3
a
2
. Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A B C ⏜ = 60 ° , S A ⊥ A B C D , S A = 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 3 a 4
B. 3 a 8 .
C. 5 a 8
D. 5 a 4 .
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
^
60
ο
, SA
⊥
(ABCD), SA
3
a
2
. Gọi O là tâm hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ^ = 60 ο ,
SA ⊥ (ABCD), SA= 3 a 2 . Gọi O là tâm hình thoi ABCD. Khoảng cách
từ điểm O đến (SBC) bằng
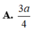
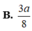
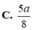
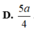
Cho hình thoi ABCD có AB = 6cm, A ^ = 60 0 . Tính diện tích của hình thoi?
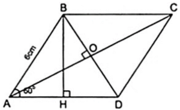
Diện tích của hình thoi ABCD là
S = 1/2AC.BD
Gọi O là giao điểm của AC và BD
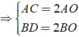
⇒ S = 2OA.OB
Từ giả thiết ta có hình thoi ABCD có A ^ = 60 0 nên Δ ABD đều
Do đó Δ ABO là nửa tam giác đều có BO = 1/2BD = 6/2 = 3( cm ).
Áo dụng định lí Py – to – go ta có:

Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
^
60
0
,
S
A
⊥
(
A
B
C
D
)
,
S
A
3
a
2
. Gọi O là tâm của hình thoi AB...
Đọc tiếp
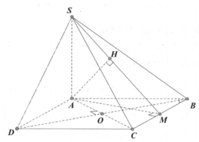
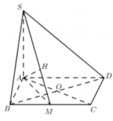
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ^ = 60 0 , S A ⊥ ( A B C D ) , S A = 3 a 2 . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng:
A. 3 a 4
B. 3 a 8
C. 5 a 8
D. 5 a 4
Chọn đáp án B.
Ta có: 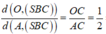
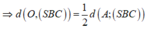
Vì AB = BC = a, ![]()
Gọi M là trung điểm BC.
Do đó: 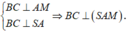
Gọi H là hình chiếu của A lên SM.
Do đó:
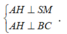
![]()
Xét tam giác SAM vuông tại A:
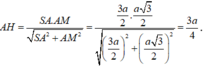
Vậy ![]()
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
^
60
0
,SA
⊥
(ABCD), SA
3
a
2
. Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng A. ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ^ = 60 0 ,SA ⊥ (ABCD), SA = 3 a 2 . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 5 a 4
B. 3 a 8
C. 5 a 8
D. 3 a 4
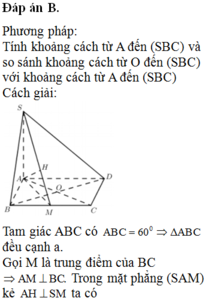
Đáp án B.
Phương pháp: Tính khoảng cách từ A đến (SBC) và so sánh khoảng cách từ O đến (SBC) với khoảng cách từ A đến (SBC)
Cách giải: Tam giác ABC có góc ABC = 600 => ∆ABC đều cạnh a.
Gọi M là trung điểm của BC => AM ⊥ BC. Trong mặt phẳng (SAM) kẻ AH ⊥ SM ta có
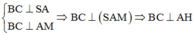
![]()
Tam giác ABC đều cạnh a nên 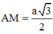
Ta có : 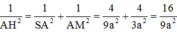
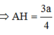
Ta có ![]()
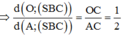
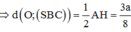
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a,
A
B
C
⏜
60
0
. Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng A.
5
a
4
B.
3
a
8...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thoi cạnh a, A B C ⏜ = 60 0 . Gọi O là tâm của hình thoi ABCD. Khoảng cách từ điểm O đến (SBC) bằng
A. 5 a 4
B. 3 a 8
C. 5 a 8
D. 3 a 4