Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

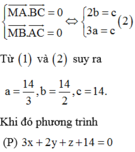
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;l). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox,Oy,Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

A. 3x+2y+z+14= 0

B. 2x+y+3z+9= 0

C. 3x+2y+z-14= 0

D. 2x+y+z-9= 0

Trong không gian với hệ toạ độ Oxyz, biết rằng có n mặt phẳng dạng ( P i ) : x + a i y + b i z + c i =0 (i=1,2,...,n) đi qua điểm M(1;2;3) và cắt các trục toạ độ lần lượt tại A,B,C khác gốc toạ độ O sao cho O.ABC là hình chóp đều. Giá trị của biểu thức  S = a 1 + a 2 + . . . + a n bằng

A. 1.

B. 3.

C. -3.

D. -1.

Trong không gian với hệ toạ độ Oxyz, có bao nhiêu mặt phẳng qua điểm M(1;1;2) và cắt trục trục toạ độ x′Ox, y′Oy,z′Oz lần lượt tại A,B,C khác gốc toạ độ O sao cho OA,OB,OC theo thứ tự lập thành một cấp số nhân và thể tích khối tứ diện OABC bằng 32 3 .

A. 3.

B. 5.

C. 2.

D. 4.

Trong không gian với hệ toạ độ Oxyz, cho ba điểm A,B,C lần lượt di động trên ba trục toạ độ Ox,Oy,Oz (không trùng với gốc toạ độ O) sao cho 1 O A 2 + 1 O B 2 + 1 O C 2 = 1 4 . Biết mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định. Tính bán kính của mặt cầu đó.

A. 4.

B. 3.

C. 1.

D. 2.

Trong không gian với hệ toạ độ Oxyz, có bao nhiêu mặt phẳng qua  M - 4 ; - 9 ; 12  và cắt các trục toạ độ  x ' Õ , y ' O y , z ' O z  lần lượt tại  A 2 ; 0 ; 0 , B , C  sao cho  O B = 1 + O C

A. 2.

B. 1.

C. 4.

D. 3.