Tính khoảng cách từ điểm M(1; 2; 0) lần lượt đến các mặt phẳng sau: ( α ): x + 2y – 2z + 1 = 0

Những câu hỏi liên quan
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
: Kinh độ của 1 điểm là
A. khoảng cách tính bằng độ từ điểm đó đến xích đạo.
B. khoảng cách tính bằng độ từ điểm đó đến cực.
C. khoảng cách tính bằng độ từ điểm đó đến vĩ tuyến đi qua điểm đó.
khoảng cách tính bằng độ từ kinh tuyến gốc đến kinh tuyến đi qua điểm đó
Xem thêm câu trả lời
Cho hai đường thẳng chéo nhau:
d
:
x
2
-
t
y
-
1
+
t
z
1
-
t
d...
Đọc tiếp
Cho hai đường thẳng chéo nhau: d : x = 2 - t y = - 1 + t z = 1 - t d ' : x = 2 + 2 t y = t z = 1 + t
Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng ( β) và khoảng cách từ M' đến mặt phẳng (α). So sánh hai khoảng cách đó.
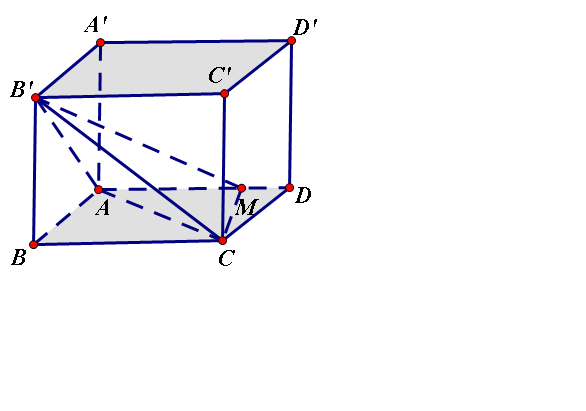
Hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, BC=2a, AA'=a. Lấy điểm M trên cạnh AD sao cho AM=3MD
1, tính khoảng cách từ B đến mp ACB'
2, tính khoảng cách từ M đến mp AB'C
ta có :
\(V_{M.AB'C}=V_{B'.MAC}=\frac{B'B.S_{ABC}}{3}\)
Mà BB'=A'A=a
\(S_{AMC}=\frac{CD.AM}{2}=\frac{a.2a}{2.3}=\frac{a^2}{3}\)
=> \(V_{M.AB'C}=\frac{a^3}{9}\) (1)
=> dM,(AB'C)=\(\frac{3.V_{M.AB'C}}{S_{AB'C}}\) (2)
tam giác AB'C cps \(AB=B'C=2\sqrt{3}\)
và \(AB=a\sqrt{2}\)
=>\(S_{AB'C}=\frac{a^2\sqrt{5}}{2}\) (3)
Từ (1), (2)&(3)
=> dM;(AB'C)=\(\frac{2a}{3\sqrt{a}}\)
Đúng 0
Bình luận (1)
Pytago tính đuợc 3 cạnh
, \(MC=\frac{a\sqrt{5}}{2}\)
Dùng công thức Heron =>\(S_{AMC}=\frac{3a^2}{4}\)
\(V_{M.AB'C}=V_{B.AB'C}=\frac{a^3}{4}\)
Mặt khác dùng công thức Heron cũng tính được \(S_{AB'C}=\frac{3a^2}{2}\)
=> \(d_{\left(M;\left(AB'C\right)\right)}=\frac{3V_{M.AB'C}}{S_{AB'C}}=\frac{a}{2}\)
Đúng 0
Bình luận (1)
tính khoảng cách từ điểm m(3;-1) đến đường thẳng delta:{x=-2+t, y=1+2t
Lời giải:
$x=-2+t; y=1+2t$
$\Rightarrow 2x-y=2(-2+t)-(1+2t)=-5$
$\Leftrightarrow 2x-y+5=0$
Khoảng cách từ điểm $M$ đến $(\Delta)$ là:
\(\frac{|2.3-(-1)+5|}{\sqrt{2^2+(-1)^2}}=\frac{12\sqrt{5}}{5}\)
Đúng 1
Bình luận (0)
a, Cho 1 điểm sáng M trước 1 gương phẳng và cách gương phẳng 2,75m. Hãy vẽ ảnh ảo của điểm sáng M và tính khoảng cách từ ảnh tới điểm sáng M.
b, Có 1 điểm B khác điểm sáng M trước gương phẳng trên. Hãy vẽ đường đi của tia tới xuất phát từ M đến gương rồi phản xạ qua B.
Hai điểm M và N gần 1 dòng diện thẳng dài . Khoảng cách từ M đến dòng điện lớn gấp 2 lần khoảng cách từ N đến dòng điện . Biết cảm ứng từ tại M có độ lớn là BM = 2.10^-5 T. Tính độ lớn của cảm ứng từ tại N.
Xem chi tiết
Ta có: \(B_M=2.10^{-7}.\dfrac{I_M}{r_M}=2.10^{-7}.\dfrac{I}{2r_N}\) (1)
\(B_N=2.10^{-7}.\dfrac{I_N}{r_N}=2.10^{-7}.\dfrac{I}{r_N}\) (2)
Từ (1) , (2) => \(\dfrac{B_M}{B_N}=\dfrac{1}{2}\Rightarrow B_N=2B_M=4.10^{-5}\left(T\right)\)
Đúng 1
Bình luận (0)
Thực hiện giao thoa ánh sáng với khe I–âng. Nguồn sáng đơn sắc có bước sóng 500 nm, khoảng cách hai khe a 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D 2 m, khoảng cách từ khe F đến mặt phẳng chứa hai khe là d 1 m. Cho khe F dao động điều hòa trên trục Ox vuông góc với trục đối xứng của hệ quanh vị trí O cách đều hai khe F1, F2với phương trình .Trên màn, xét điểm M cách vân trung tâm một khoảng 1 mm. Tính cả thời điểm t 0, điểm M trùng với vân sáng lần thứ 2018 vào thời điểm...
Đọc tiếp
Thực hiện giao thoa ánh sáng với khe I–âng. Nguồn sáng đơn sắc có bước sóng 500 nm, khoảng cách hai khe a =1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 2 m, khoảng cách từ khe F đến mặt phẳng chứa hai khe là d =1 m. Cho khe F dao động điều hòa trên trục Ox vuông góc với trục đối xứng của hệ quanh vị trí O cách đều hai khe F1, F2với phương trình
.Trên màn, xét điểm M cách vân trung tâm một khoảng 1 mm. Tính cả thời điểm t = 0, điểm M trùng với vân sáng lần thứ 2018 vào thời điểm
A. 252(s)
B. 504+ 1/2 (s)
C. 252+ 1/6 (s)
D. 252+ 1/12 (s)
Đáp án D
Khi dịch chuyển nguồn theo phương song song với hai khe thì hệ vân (vân trung tâm ) dịch chuyển theo chiều ngược lại một đoạn :
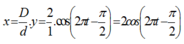
Chu kì dao động là : T = 1s.
Khoảng vân : 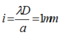
Điểm M cách vị trí trung tâm 1mm, vậy ban đầu khi t = 0 thì M là vân sáng.
Điểm M là vân sáng thì thỏa mãn : xM = ki
Ta thấy vân trung tâm sẽ dao động với biên độ 2 cm (từ phương trình), vậy điểm M sẽ là vân sáng khi vân trung tâm ở các vị trí có tọa độ x = 0, 1, 2, – 1, –2 cm
Vẽ đường tròn ta được:
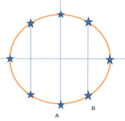
Các vị trí đánh dấu sao là các vị trí trong một chu kì chuyển động M là vân sáng. Ban đầu M nằm ở vị trí A. mỗi chu kì có 8 lần M là vân sáng
Vậy khi M à vân sáng lần thứ 2018 = 8.252 + 2 lần thì nó đã đi trong thời gian là : t = 252T + ∆t
Dễ thấy khi đi được 252 chu kì thì M đã quay lại A, vậy chỉ cần đi đến B là đã được thêm 2 lần nữa ( vì ban đầu khi t = 0 thì M ở A, nên nó là 1 vân sáng, đến lúc nó đến B được tính là lần nữa).
Thời gian đi hết cung AB là :
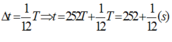
Đúng 0
Bình luận (0)
Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là 4,5 m. Từ một điểm M trên thân cổng, người ta đo được khoảng cách từ điểm đó đến mặt đất(điểm H)là 1,8 m và khoảng cách từ điểm H đến chân cổng gần nhất là 1 m. Tính chiều cao của cổng theo đơn vị mét,làm tròn tới hàng phần mười.
Xem chi tiết























