Khoảng cách từ điểm M(3;-4) đến đường thẳng D: 3x-4y-1=0 bằng
A. 8 5
B. 24 5
C. 5
D. 7 5
Những câu hỏi liên quan
Khoảng cách từ một điểm sáng S đến gương phẳng bằng 0,5m. Hỏi khoảng cách từ điểm sáng S đến ảnh S’ của nó tạo bởi gương phẳng bằng bao nhiêu?
A.
4 m
B.
3 m
C.
2 m
D.
1 m
điểm 1 nằm trên một đường thẳng. Điểm 2 nằm bên phải điểm 1. Điểm 3 nằm bên phải điểm 2. Khoảng cách từ điểm 1 đến điểm 2 bằng khoảng cách từ điểm 2 đến điểm 3, v.v ... Cuối cùng, điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 bằng khoảng cách từ điểm 99 đến điểm 100. Nếu khoảng cách từ điểm 1 đến điểm 101 là 1m thì khoảng cách từ điểm 13 đến điểm 31 là bao nhiêu cm?
Đọc tiếp
điểm 1 nằm trên một đường thẳng. Điểm 2 nằm bên phải điểm 1. Điểm 3 nằm bên phải điểm 2. Khoảng cách từ điểm 1 đến điểm 2 bằng khoảng cách từ điểm 2 đến điểm 3, v.v ... Cuối cùng, điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 bằng khoảng cách từ điểm 99 đến điểm 100. Nếu khoảng cách từ điểm 1 đến điểm 101 là 1m thì khoảng cách từ điểm 13 đến điểm 31 là bao nhiêu cm?
Trả lời:
Từ điền số 1 đến điểm 101 sẽ có: 101-1=100 khoảng bằng nhau.=> mỗi một khoảng bằng nhau có độ dài= 1m/100= 100cm/100=1cm
Từ điểm 13 đến điểm 31 có (31-13)=18 khoảng bằng nhau
=> Khoảng cách từ điểm 13 đến điểm 31 là: 18x1 cm= 18cm
Không có gì ! Chúc bạn học tốt nha
tk you so much
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng.
Đọc tiếp
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng.
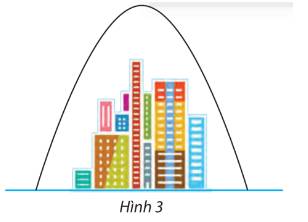
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
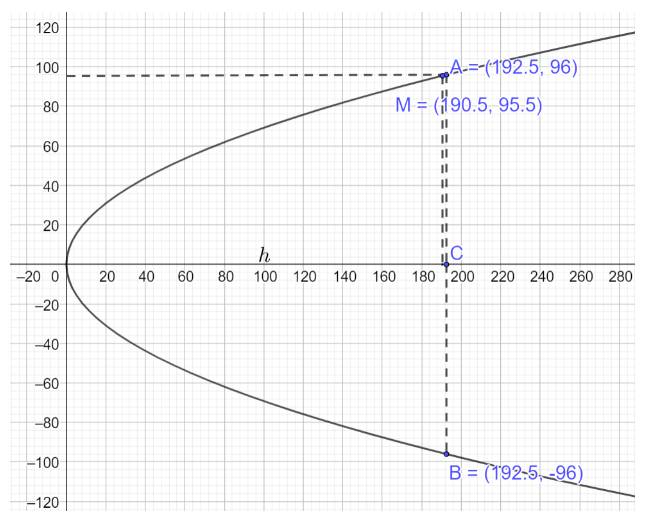
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m
Đúng 0
Bình luận (0)
19 tháng 12 2023 lúc 19:32
Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là 4,5 m. Từ một điểm M trên thân cổng, người ta đo được khoảng cách từ điểm đó đến mặt đất(điểm H)là 1,8 m và khoảng cách từ điểm H đến chân cổng gần nhất là 1 m. Tính chiều cao của cổng theo đơn vị mét,làm tròn tới hàng phần mười.
Xem chi tiết
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.Đồ thị (C) của hàm số
y
x
+
2
x
-
3
Đọc tiếp
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Đồ thị (C) của hàm số y = x + 2 x - 3
Giả sử M( x o ; y o ) ∈ (C). Gọi d 1 là khoảng cách từ M đến tiệm cận đứng và d 2 là khoảng cách từ M đến tiệm cận ngang, ta có:
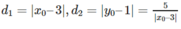
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x o = 3 + 5 hoặc x o = 3 - 5
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy). A. 12 B. 5 C. 2 D. 6
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M thỏa mãn OM = 7. Biết rằng khoảng cách từ M đến (Oxz), (Oyz) lần lượt là 2 và 3. Tính khoảng cách từ M đến (Oxy).
A. 12
B. 5
C. 2
D. 6
Đáp án D
Gọi M ( a ; b ; c ) ⇒ d M , O x z = b = 2 ; d M , O y z = a = 3
Do O M = 7 ⇒ a 2 + b 2 + c 2 = 49 ⇒ c = 49 - a 2 - b 2 = 6
Vậy d M ; O x y = 6 .
Đúng 0
Bình luận (0)
Thực hiện giao thoa Young. Nguồn sáng đơn sắc có bước sóng 400 nm, khoảng cách hai khe a 1 nm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D 3 m. Trên màn, xét điểm M cách vân trung tâm một khoảng 10 mm. Dịch chuyển màn quan sát từ từ lại gần mặt phẳng chứa hai khe thêm một đoạn 1 m thì điểm M chuyển thành vân tối A. 4 lần. B. 5 lần. C. 3 lần D. 2 lần.
Đọc tiếp
Thực hiện giao thoa Young. Nguồn sáng đơn sắc có bước sóng 400 nm, khoảng cách hai khe a = 1 nm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 3 m. Trên màn, xét điểm M cách vân trung tâm một khoảng 10 mm. Dịch chuyển màn quan sát từ từ lại gần mặt phẳng chứa hai khe thêm một đoạn 1 m thì điểm M chuyển thành vân tối
A. 4 lần.
B. 5 lần.
C. 3 lần
D. 2 lần.
Đáp án B
Phương pháp: Sử dụng điều kiện vân sáng tối trong giao thoa khe Yang
Cách giải: Khi ta thay đổi khoảng cách từ hai khe đến màn làm thay đổi khoảng vân I, do đó tại M lần lượt sẽ chuyển thành vân tối, sáng. Điều kiện để tại M là vân tối là:
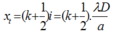
Suy ra khoảng cách D được xác định là:
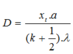
Ta xét điểm M thỏa mãn điều kiện là vân tối, và khoảng cách D thay đổi từ giá trị 3 m đến 2m. suy ra điều kiện với D là:
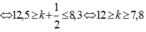
Vì k là số nguyên nên có các giá trị k thỏa mãn là: k = 8,9,10,11,12.
Có 5 giá trị thỏa mãn, tức là có 5 lần M trở thành vân tối.
Đúng 0
Bình luận (0)
Thực hiện giao thoa Young. Nguồn sáng đơn sắc có bước sóng 400 nm, khoảng cách hai khe a 1 nm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D 3 m. Trên màn, xét điểm M cách vân trung tâm một khoảng 10 mm. Dịch chuyển màn quan sát từ từ lại gần mặt phẳng chứa hai khe thêm một đoạn 1 m thì điểm M chuyển thành vân tối A. 4 lần B. 5 lần C. 3 lần D. 2 lần
Đọc tiếp
Thực hiện giao thoa Young. Nguồn sáng đơn sắc có bước sóng 400 nm, khoảng cách hai khe a = 1 nm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 3 m. Trên màn, xét điểm M cách vân trung tâm một khoảng 10 mm. Dịch chuyển màn quan sát từ từ lại gần mặt phẳng chứa hai khe thêm một đoạn 1 m thì điểm M chuyển thành vân tối
A. 4 lần
B. 5 lần
C. 3 lần
D. 2 lần
Đáp án B
Phương pháp: Sử dụng điều kiện vân sáng tối trong giao thoa khe Yang
Cách giải: Khi ta thay đổi khoảng cách từ hai khe đến màn làm thay đổi khoảng vân I, do đó tại M lần lượt sẽ chuyển thành vân tối, sáng. Điều kiện để tại M là vân tối là:
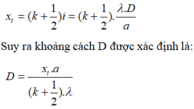
Ta xét điểm M thỏa mãn điều kiện là vân tối, và khoảng cách D thay đổi từ giá trị 3 m đến 2m. suy ra điều kiện với D là:
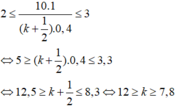
Vì k là số nguyên nên có các giá trị k thỏa mãn là: k = 8,9,10,11,12.
Có 5 giá trị thỏa mãn, tức là có 5 lần M trở thành vân tối.
Đúng 0
Bình luận (0)
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
Đúng 2
Bình luận (0)
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15