Bài 2 : Lập phương trình đường thẳng đi qua M(2;-3) và cắt Ox, Oy tại A,B sao cho
a) OA=2/3OB
b) 4OA2 +OB2 =100
c) SOAB đạt GTLN
d) \(\frac{3}{OA^2}+\frac{2}{OB^2}=\frac{275}{36}\)
Bài 4.
a) Lập phương trình đường thẳng (d) đi qua điểm M (-1; 3) và có hệ số góc bằng 2.
b) Lập phương trình đường thẳng (d) đi qua M(3; 5) và song song với đường thẳng (d’) có phương trình y = 2x
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
c) Lập phương trình đường thẳng (d) đi qua M(3; 5) và/vg/goc với đường thẳng (d’) có phương trình y = 2x
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
c) Lập phương trình đường thẳng (d) đi qua M(3; 5) và/vg/goc với đường thẳng (d’) có phương trình y = 2x
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
giúp/mik/mik/đang/cần/gấp/ạ
c) Lập phương trình đường thẳng (d) đi qua M(3; 5) và/vg/goc với đường thẳng (d’) có phương trình y = 2x
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
c) Lập phương trình đường thẳng (d) đi qua M(3; 5) và/vg/goc với đường thẳng (d’) có phương trình y = 2x
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
c)
(d) vuông góc với (d') : y = 2x
=> (d) có dạng : y = -2x + b
(d) đi qua M (3,5) :
5 = (-2) . 3 + b
=> b = 10
(d) : y = -2x + 10
d)
Gọi : hàm số có dạng : y = ax + b
Hàm số đi qua điểm A ( 1,2) , B(2,1) nên :
\(\left\{{}\begin{matrix}2=a+b\\1=2a+b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\)
e)
(d) đi qua gốc tọa độ O :
=> d : y = ax
(d) đi qua điểm A(1;2) nên :
2 = a * 1
=> a = 2
(d) : y = 2x
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
Lập phương trình đường thẳng đi qua hai điểm M(\(-\dfrac{2}{3}\);-7) và N(2;1)
Vì (d): y=ax+b đi qua M(-2/3;-7) và N(2;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}-\dfrac{2}{3}a+b=-7\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-5\end{matrix}\right.\)
\(\overrightarrow{MN}\)=(8/3;8)=8/3.(1;3).
Phương trình đường thẳng cần tìm đi qua N(2;1) và nhận vectơ \(\overrightarrow{n}\)=(3;-1) làm một vectơ pháp tuyến.
MN: 3(x-2)-1(y-1)=0 \(\Leftrightarrow\) 3x-y-5=0.
Lập phương trình tham số của đường thẳng: Đi qua M(2 ; 3 ; -5) và song song với đường thẳng (Δ): ∆ : x = - 2 + 2 t y = 3 - 4 t z = - 5 t
(Δ) nhận 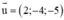 là 1 vtcp
là 1 vtcp
+ (d) cần tìm song song với (Δ)
⇒ (d) nhận 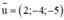 là 1 vtcp
là 1 vtcp
+ (d) đi qua M(2; 3; -5)
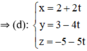
| Bài 2. Lập phương trình của đường thẳng y= ax+b | biết rằng đường thẳng: |
a. Có hệ số góc bằng -2 và đi qua điểm A( 3,5) .
b. Cắt trục tung tại điểm có tung độ bằng -3 , cắt trục hoành tại điểm có hoành độ bằng 2.
c. Đi qua hai điểm M( 2,3) và N(-1,4).
d. Đi qua hai điểm E( 4,-3) và F( -2, 5) .
e. Đi qua gốc O và điểm B(-1, 3) .
f. Song song với y = 3-2x và đi qua điểm C(-2,1)
g. Vuông góc với đường thẳng y= 1/3 x - 7/3 và cắt trục tung tại điểm có tung độ bằng 4
bài 1: a) Tìm m để đường thẳng (d) có phương trình y=5x-3m+1 đi qua điểm A(1;-3)
b) Tìm phương trìn đường thẳng (d1) song song vs (d2) có phương trình y=3x-2 và căt trục hoành tại điểm có hoành độ =2
bài 2: Tìm m để đường thẳng y=(2m-5)x-5m đi qua diểm thuộc đường thẳng y=x+5 có tung độ =2
a, Vì A(1;-3) năm trên đường thẳng (d) khi tọa độ điểm B thỏa mãn phương trình đường thẳng (d)
Thay x = 1 ; y = -3 vào (d) phương trình tương đương
\(-3=5-3m+1\Leftrightarrow4-3x=-3\Leftrightarrow-3x=-7\Leftrightarrow x=\frac{7}{3}\)
b ; c thiếu đề
Bài 2 :
Vì y = x + 5 có tung độ là 2
=> y = 2 + 5 = 7
Vậy y = ( 2m - 5 )x - 5m đi qua đường thẳng y = x + 5 A( 2 ; 7 )
Thay x = 2 ; y = 7 vào y = ( 2m - 5 )x - 5m ta được :
\(7=\left(2m-5\right)2-5m\Leftrightarrow4m-10-5m=7\Leftrightarrow-m=17\Leftrightarrow m=-17\)