Cho tam giác ABC có : C(0;-2) Pt đường cao AH : x+2y-1=0 Pt trung tuyến BN : -x+y=0 Tìm tọa độ A,B

Những câu hỏi liên quan
Trong không gian Oxyz cho tam giác ABC có tọa độ các đỉnh là:
A(a; 0; 0), B(0; b; 0), C(0; 0; c)
Chứng minh rằng tam giác ABC có ba góc nhọn.
Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.
Đúng 0
Bình luận (0)
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
Cho tam giác ABC có A(-1;0),B(4;0),C(0;m), m≠0. Gọi G là trọng tâm của tam giác ABC. Xác định m để tam giác GAB vuông tại G
Cho tam giác ABC có A(-1;0) , B(4;0) , C(0;m) và m khác 0. Gọi G là trọng tâm của tam giác ABC. Xđ m để tam giác GAB vuông tại G
Tọa độ trọng tâm G của ΔABC là \(G\left(1;\dfrac{m}{3}\right)\)
⇒ \(\left\{{}\begin{matrix}\overrightarrow{AG}=\left(2;\dfrac{m}{3}\right)\\\overrightarrow{BG}=\left(-3;\dfrac{m}{3}\right)\end{matrix}\right.\)
Để ΔGAB vuông tại G
⇒ GA ⊥ GB
⇒ \(\overrightarrow{GA}\) ⊥ \(\overrightarrow{GB}\)
⇒ \(\overrightarrow{GA}.\overrightarrow{GB}=0\)
⇒ 2 . (-3) + \(\dfrac{m^2}{9}\) = 0
⇒ m2 = 6 . 9 = 54
⇒ m = \(\pm\sqrt{54}\)
Mình chắc chắn cách làm của mình là đúng còn về tính toán thì chưa chắc nên bạn tự kiểm tra nhá ![]()
Đúng 1
Bình luận (0)
Cho tam giác ABC có A(-1; 1), B(0; 2), C(1; 1). Trực tâm của tam giác ABC có tọa độ là
A.(0; 2)
B. (0; 1)
C. (1; 0)
D. (1; 1)
Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(1; -1) ; B(3; -3) và C(6; 0). Diện tích tam giác ABC là:
A. 12
B. 6
C. 6 2
D. 9
Chọn B.
Ta có:
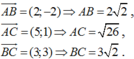
Mặt khác ![]()
Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.
Đúng 0
Bình luận (0)
Cho tam giác ABC có A( -1; 3) ; B( -2; 0) và C( 5;1). Trực tâm H của tam giác ABC có toạ độ là:
A. (3 ; -1)
B. (-1 ; 3)
C. (2 ; -1)
D. (2 ; -3)
Ta có:
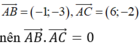
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.
Đúng 0
Bình luận (0)
cho \(\Delta ABC\) có \(\widehat A={40^0}\) biết \(\widehat B= 3\widehat C\) tam giác abc là tam giác gì
giúp mik với
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(6;-2) pt phân giác ngoài góc C là x+y+8=0 và pt trung trực BC là 2x+4y+3=0. Lập pt các cạnh tam giác ABC
Cho tam giác ABC có A(2;-3) , B(3;-2). Trọng tâm tam giác ABC thuộc đt d:3x-y-8=0. Tìm tọa độ điểm C biết diện tích tam giác ABC =3/2
Xem chi tiết
Gọi \(C\left(x;y\right)\) và G là trọng tâm tam giác
\(\Rightarrow\left\{{}\begin{matrix}x_G=\dfrac{x+5}{3}\\y_G=\dfrac{y-5}{3}\end{matrix}\right.\) \(\Rightarrow3\left(\dfrac{x+5}{3}\right)-\dfrac{y-5}{3}-8=0\)
\(\Leftrightarrow3x-y-4=0\) \(\Rightarrow y=3x-4\Rightarrow C\left(x;3x-4\right)\)
\(S_{ABC}=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
\(\Leftrightarrow\dfrac{3}{2}=\dfrac{1}{2}\left|5\left(3x-1\right)-\left(x-2\right)\right|\)
\(\Leftrightarrow x=...\)
Đúng 1
Bình luận (0)
















