Cho z 1 = 1 - 3 i ; z 2 = 2 + i ; z 3 = 3 - 4 i . Tính z 1 z 2 z 3 + z 2 2 z 3
A. 20 - 35i
B. 20 + 35i
C. -20 + 35i
D. -20 - 35i
Cho z = 3(1 + i) - 4(1-i). Tìm |z|
A. |z| = 5 2
B. |z| = 5
C. |z| = 7
D. |z| = 50
Câu 1: Tìm phần thực phần ảo của Z thỏa mãn 1+(1+i)+(1+i^2)+...+(1+i)^20
Câu 2: Tìm 1/Z sao cho Z=(3+căn3 i)^3
Câu 3: Tìm Z thỏa mãn môđun (Z-1)/(Z+1)=1 hoặc môđun (Z-3i)/(Z+1)=1
1/Áp dụng công thức tổng cấp số nhân:
\(z=1+\left(1+i\right)+\left(1+i\right)^2+...+\left(1+i\right)^{20}=1+\frac{\left(1+i\right)^{21}-1}{i+1-1}=1+\frac{\left(1+i\right)^{21}-1}{i}\)
Ta có:
\(\left(1+i\right)^{21}=\left(1+i\right)\left[\left(1+i\right)^2\right]^{10}=\left(1+i\right)\left(1+2i+i^2\right)^{10}\)
\(=\left(1+i\right)\left(2i\right)^{10}=\left(1+i\right).2^{10}.i^{10}=\left(1+i\right)2^{10}\left(i^2\right)^5=-\left(1+i\right).2^{10}\)
\(\Rightarrow z=1+\frac{-\left(1+i\right)2^{10}-1}{i}=1+\frac{-i\left(1+i\right)2^{10}-i}{i^2}=1+\left(i+i^2\right)2^{10}+i=1+i+\left(i-1\right).2^{10}\)
\(\Rightarrow z=\left(1-2^{10}\right)+\left(1+2^{10}\right)i\)
2/
\(z=\left(3+i\sqrt{3}\right)^3\Rightarrow\frac{1}{z}=\frac{1}{\left(3+i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(3+i\sqrt{3}\right)^3\left(3-i\sqrt{3}\right)^3}=\frac{\left(3-i\sqrt{3}\right)^3}{\left(9-3i^2\right)^3}\)
\(\Rightarrow\frac{1}{z}=\frac{\left(3-i\sqrt{3}\right)^3}{12^3}=\left(\frac{1}{4}-\frac{\sqrt{3}}{12}i\right)^3\)
3/ Bạn viết lại đề được không?
Cho hai số phức z = (2x+3) + (3y-1)i và z' = (y-1)i. Ta có z = z' khi:
A . x = 3 2 ; y = 0
B . x = - 3 2 ; y = 0
C . x = 3 ; y = 1 3
D . x = 0 ; y = - 3 2
Cho hai số phức z=(2x+3) + (3y-1)i và z'=3x + (y+1)i. Khi z=z', chọn khẳng định đúng.
![]()
![]()
![]()
![]()
a, Cho x2 + y2 + z2 + 3 = 2(x + y + z). CMR x = y = z = 1
b, CMR 20053 + 125 chia hết cho 2010
c, CMR x6 - 1 chia hết cho x + 1 và x - 1
\(x^6-1=\left(x^3-1\right)\left(x^3+1\right)=\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)\left(x^2-x+1\right)\\ \RightarrowĐPCM\)
\(2005^3+125=\left(2005+5\right)\left(2005^2+2005\cdot5+5^2\right)=2010\left(2005^2+2005\cdot5+5^2\right)⋮2010\)\(x^2+y^2+z^2+3=2\left(x+y+z\right)\\ \Leftrightarrow x^2+y^2+x^2+3=2x+2y+2z\\ \Leftrightarrow x^2-2x+1+y^2-2y+1+z^2-2z+1=0\\ \Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=0\\ \left(x-1\right)^2\ge0;\left(y-1\right)^2\ge0;\left(z-1\right)^2\ge0\\ \Rightarrow\left(x-1\right)^2=\left(y-1\right)^2=\left(z-1\right)^2=0\\ \Rightarrow x-1=y-1=z-1=0\\ \Leftrightarrow x=y=z=1\)
b) \(2005^3+125\)
\(=2005^3+5^3\)
\(=\left(2005+5\right)\left(2005^2-2005.5+5^2\right)\)
\(=2010\left(2005^2-2005.5+5^2\right)\)\(⋮\) 2010
Vậy \(2005^3+125\) chia hết cho 2010
c) \(x^6-1\)
\(=\left(x^3\right)^2-1^2\)
\(=\left(x^3-1\right)\left(x^3+1\right)\)
\(=\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)\left(x^2-x+1\right)\) \(⋮\) \(\left(x-1\right)\) và \(\left(x+1\right)\)
Vậy \(x^6-1\) chia hết cho \(\left(x-1\right)\) và \(\left(x+1\right)\)
Cho các số phức z và w thỏa mãn ( 3 - i ) | z | = z w - 1 + 1 - i . Tìm GTLN của T = | w + i |
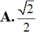
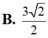
![]()
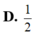
Cho các số phức z và w thỏa mãn ( 3 - i ) z = z w - 1 + 1 - i . Tìm GTLN của T = w + i .
A. 2 2
B. 3 2 2
C. 2
D. 1 2
cho x, y, z dương thỏa mãn x+y+z=1 và x^3 + y^3 + z^3 =1 .Tính H=x^2007 +y^2007 + z^2007
GIÚP MÌNH NHA!...
cho x + y + z = 1
x 2+ y2 + z2 = 1
xyz=1
chứng minh rằng: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=1\)
Hình như đề có vấn đề đó bạn
theo mình
Có : x+y+z =1
\(\Rightarrow\)\(x^2+y^2+z^2+2xz+2yz+2xy=1\)
\(\Leftrightarrow\)xy+xz+zy =0
Lại có : \(x^3+y^3+z^3-3xyz=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=1\left(1-0\right)=1\)
\(x^3+y^3+z^3=1+3=4\)
\(\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=4\)
Cho số phức z thoả mãn |z-1-i|=1 Khi 3|z|=2|z-4-4i| đạt giá trị lớn nhất. Tính |z|
A. 2 - 1
B. 2
C. 2 + 1
D. 3
Đặt ![]()
![]()
![]()
Khi đó
![]()
![]()
![]()
![]()
![]()
![]()

Dấu bằng đạt tại
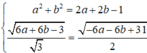
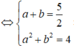
![]()
Chọn đáp án B.