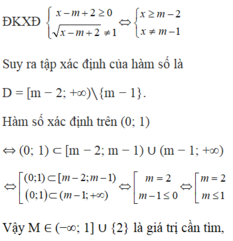cho hàm số y=x2-2(m+1/m)x+m (m>0) xác định trên [-1;1] . giá trị lớn nhất , giá trị nhỏ nhất của hàm số trên [-1;1] lần lượt là y1 ; y2 thoản mãn y1-y2=8

Những câu hỏi liên quan
Cho hàm số y
x
2
− 2(m +
1
m
)x + m (m 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là
y
1
,
y
2
thỏa mãn
y
1
-
y
2
8. Khi đó giá trị của m bằng A. m 1 B. m
∈...
Đọc tiếp
Cho hàm số y = x 2 − 2(m + 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y 1 , y 2 thỏa mãn y 1 - y 2 = 8. Khi đó giá trị của m bằng
A. m = 1
B. m ∈ ∅
C. m = 2
D. m = 1, m = 2
Xác định giá trị của tham số m để hàm số
y
x
2
+
m
+
1
x
-
1
2
-
x...
Đọc tiếp
Xác định giá trị của tham số m để hàm số y = x 2 + m + 1 x - 1 2 - x
nghịch biến trên mỗi khoảng xác định của nó
A. m = −1; B. m > 1;
C. m ∈ (−1;1); D. m ≤ −5/2.
Đáp án: D.
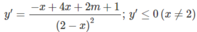
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.
Đúng 0
Bình luận (0)
Cho hàm số:
y
m
x
x
−
m
+
2
−
1
với m là tham số. Tìm m để hàm số xác định trên (0; 1) A. M
∈
(
−
∞
;
3
2
]
∪
{
2...
Đọc tiếp
Cho hàm số: y = m x x − m + 2 − 1 với m là tham số. Tìm m để hàm số xác định trên (0; 1)
A. M ∈ ( − ∞ ; 3 2 ] ∪ { 2 }
B. M ∈ ( − ∞ ; - 1 ] ∪ { 2 }
C. M ∈ ( − ∞ ; 1 ] ∪ { 3 }
D. M ∈ ( − ∞ ; 1 ] ∪ { 2 }
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
Δ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 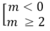
Đúng 0
Bình luận (0)
Xác định giá trị của tham số m để hàm số sau không có cực trịy m
x
3
/3 + m
x
2
+ 2(m - 1)x - 2.A. m
≤
0 hoặc m
≥
2 B. m
≥
0C. m
≤
0
≤
2 D. m ∈ [0; +
∞
]
Đọc tiếp
Xác định giá trị của tham số m để hàm số sau không có cực trị
y = m x 3 /3 + m x 2 + 2(m - 1)x - 2.
A. m ≤ 0 hoặc m ≥ 2 B. m ≥ 0
C. m ≤ 0 ≤ 2 D. m ∈ [0; + ∞ ]
Đáp án: A.
- Nếu m = 0 thì y = -2x - 2, hàm số không có cực trị.
- Nếu m ≠ 0: Hàm số không có cực trị khi và chỉ khi phương trình y' = m x 2 + 2mx + 2(m - 1) = 0 không có hai nghiệm phân biệt. Muốn vậy, phải có
∆ ' = m 2 - 2m(m - 1) = - m 2 + 2m ≤ 0
⇔ 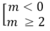
Đúng 0
Bình luận (0)
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Hàm số
y
1
3
x
3
+
(
m
+
1
)
x
2
-
(
m
+
1
)
x
+
1
đồng biến trên tập xác định của nó khi: A. -2 ≤ m ≤ -1 B. -2 m -1 C. m -2 D. m -1
Đọc tiếp
Hàm số y = 1 3 x 3 + ( m + 1 ) x 2 - ( m + 1 ) x + 1 đồng biến trên tập xác định của nó khi:
A. -2 ≤ m ≤ -1
B. -2 < m < -1
C. m < -2
D. m > -1
Hàm số
có tập xác định: D = R.
y ' = x 2 + 2 ( m + 1 ) x - m - 1
Để hàm số đã cho đồng biến trên R khi và chỉ khi:
y ' = f ( x ) = x 2 + 2 ( m + 1 ) x - m - 1 ≥ 0 ∀ x ∈ R
⇔ -2 ≤ m ≤ -1
Chọn A
Đúng 0
Bình luận (0)
Hàm số
y
-
1
3
x
3
-
(
m
+
1
)
x
2
+
(
m
+
1
)
x
+
1
nghịch biến trên tập xác định của nó khi: A.
-
2
m
-
1
B.
m
-
2
C.
m
-
1
D.
-...
Đọc tiếp
Hàm số y = - 1 3 x 3 - ( m + 1 ) x 2 + ( m + 1 ) x + 1 nghịch biến trên tập xác định của nó khi:
A. - 2 < m < - 1
B. m < - 2
C. m > - 1
D. - 2 ≤ m ≤ - 1
Cho hàm số y = (2015 – m )x2. Xác định m để hàm số nghịch biến khi x > 0.
Để hàm số nghịch biến khi x>0 thì 2015-m<0
=>m>2015
Đúng 0
Bình luận (0)