(d1): 2x + y - 3 = 0

y = -2x + 2

(d2): y = 5 - 2x

y = -2x + 5

(d3): 2y = x + 4

y = x/2 + 2

(d4): x + y - 1 = 0

y = -x + 1

*) Cặp đường thẳng song song:

(d1) và (d2)

*) Các cặp đường thẳng cắt nhau:

(d1) và (d3); (d1) và (d4); (d2) và (d3); (d2) và (d4); (d3) và (d4)

\(\left(1\right)\cap\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5\ne2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne4\\m\ne\dfrac{3}{5}\end{matrix}\right.\\ \left(1\right)//\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow m=4\\ \left(1\right)\equiv\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

a). Để hai hàm số cắt nhau thì:

   a≠a'⇒ m+5=2m+1

⇔ m+5=2m+1

⇔ m-2m=1-5

⇔  -m    = -4

⇔  m     = 4.

Vậy hai hàm số cắt nhau khi m =4.

b). Để hai hàm số song song khi:

\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\)

Vậy hai hàm số đó song song khi m=-4; m≠\(\dfrac{3}{5}\).

c). Để hai hàm số trùng nhau khi:

\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m=\dfrac{3}{5}\end{matrix}\right.\)

Vậy hai hàm số đó trùng nhau khi m=-4; m=\(\dfrac{3}{5}\).

a: Phương trình hoành độ giao điểm là:

-3x-3=-2x

=>-3x+2x=3

=>-x=3

=>x=-3

Thay x=-3 vào y=-2x, ta được:

\(y=-2\cdot\left(-3\right)=2\cdot3=6\)

Vậy: Hai đường thẳng y=-3-3x và y=-2x cắt nhau tại điểm A(-3;6)

b: Phương trình hoành độ giao điểm là:

\(3\left(x-1\right)-5x=-\sqrt{5}\cdot x-2\)

=>\(-2x-3=-\sqrt{5}\cdot x=-2\)

=>\(-2x+x\cdot\sqrt{5}=-2+3=1\)

=>\(x\left(\sqrt{5}-2\right)=1\)

=>\(x=\dfrac{1}{\sqrt{5}-2}=\sqrt{5}+2\)

Thay \(x=\sqrt{5}+2\) vào y=3(x-1)-5x, ta được:

\(y=3x-3-5x=-2x-3=-2\cdot\left(\sqrt{5}+2\right)-3\)

\(=-2\sqrt{5}-4-3=-2\sqrt{5}-7\)

Vậy: Tọa độ giao điểm của hai đường thẳng \(y=-x\sqrt{5}-2;y=3\left(x-1\right)-5x\) là \(B\left(\sqrt{5}+2;-2\sqrt{5}-7\right)\)

+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= -5( x+ 1) và y=3x+a :

-5x-5=3x+a  suy ra -8x-a=5           (1)

+ Phương trình hoành độ giao điểm giữa hai đường thẳng y= 3x+a và y=ax+3là:

ax+3=3x+a hay (a-3) x=a-3

suy ra x=1( vì a≠3).

+Thế x= 1 vào (1) ta được: -8-a=5 nên a= -13.

Chọn D.

a: 

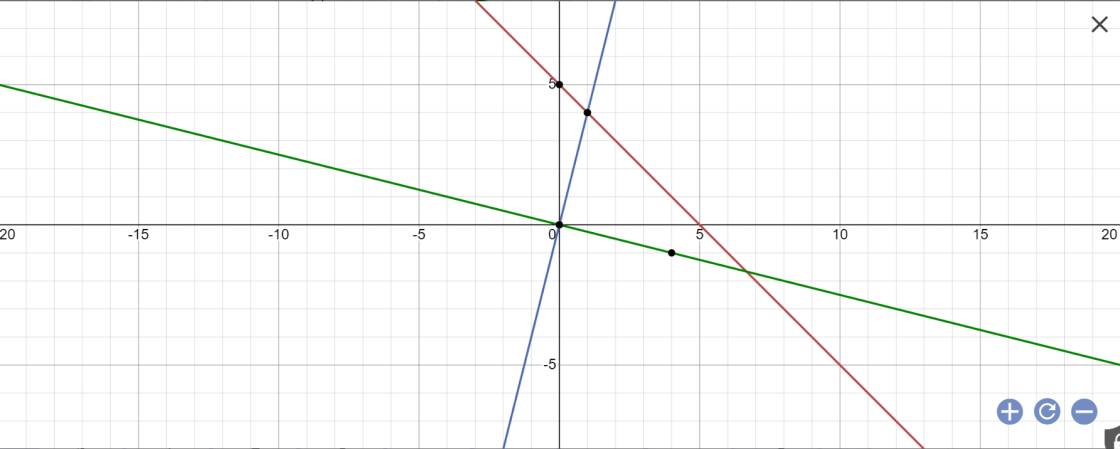
b: tọa độ A là;

-x+5=4x và y=4x

=>x=1 và y=4

Tọa độ B là;

-x+5=-1/4x và y=-1/4x

=>-3/4x=-5 và y=-1/4x

=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3

=>B(20/3;-5/3)

c: O(0;0); A(1;4); B(20/3;-5/3)

\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)

\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)

\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)

\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)

=>góc AOB tù

=>ΔOAB tù

đường thẳng y = ax+ b song song với đường thằng y = -x+ 5

=> a = -1 ; b khác 5

=> đường thẳng có dạng y = -x + b

gọi A là giao của đg thẳng y = -x + b và parabol
=> x_A = 1 => y_A = x_A² = 1 

A(1; 1) thuộc đg thẳng y = -x + b => y_A = - x_A + b =>b = 2 (thoả mãn)

Đáp án là B