Cho hàm số
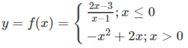
Tính giá trị của hàm số đó tại x = 5; x = -2; x = 0; x = 2
Những câu hỏi liên quan
Cho hàm số y = 1/9 x 2 . Giá trị của hàm số đó tại x = 3 2 là:
A. 1
B. 2
C. -2
D. 3 2
Chọn đáp án B
Thay x = 3 2 vào y = 1/9 x 2 ta được:
y= 1/9 3 2 2 = 1/9.18 = 2
Đúng 0
Bình luận (0)
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔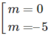 
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔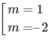 
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
(
1
-
x
+
x
2
)
10
Giá trị đạo hàm cấp 5 của hàm số tại
x
o
1
là A. 34848 B. 30240 C. 125240 D. 174240
Đọc tiếp
Cho hàm số f ( x ) = ( 1 - x + x 2 ) 10 Giá trị đạo hàm cấp 5 của hàm số tại x o = 1 là
A. 34848
B. 30240
C. 125240
D. 174240
Cho hàm số y f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng? A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số. B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y f(x).
C. Số M f(
x
0
) trong đó
x
0
∈ D là giá trị lớn nhất của hàm số y f(x) nếu M f(x), ∀x ∈ D D. Nếu tồn tại
x
0
∈ D...
Đọc tiếp
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
Đúng 0
Bình luận (0)
Cho hàm số y=(m+1)x
a) Tìm các giá trị của tham số m để tham số nhận giá trị bằng -5 tại x=5 ,
b) Với giá trị nào của m thì đồ thị hàm số đi qua điểm A(2;3)?
c)Tìm giá trị của m để điểm B(0;4) thuộc đồ thị hàm số.
Cho hàm số
y
f
x
x
+
1
v
ớ
i
x
≥
2
x
2
-...
Đọc tiếp
Cho hàm số
y = f x = x + 1 v ớ i x ≥ 2 x 2 - 2 v ớ i x < 2
Tính giá trị của hàm số đó tại x = 3; x = -1; x = 2.
- Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.
- Ta có : x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.
- Ta có : x = 2 nên f(2) = 2 + 1 = 3.
Đúng 0
Bình luận (0)
Cho hàm số y
x
3
+
3
m
x
2
-
2
x
+
1
. Hàm số có điểm cực đại tại x -1 khi đó giá trị của tham số m thỏa mãn A. m
∈
(-1;0) B. m
∈
(0;1) C. m
∈
(-3;-1) D. m
∈
(1;3)
Đọc tiếp
Cho hàm số y = x 3 + 3 m x 2 - 2 x + 1 . Hàm số có điểm cực đại tại x = -1 khi đó giá trị của tham số m thỏa mãn
A. m ∈ (-1;0)
B. m ∈ (0;1)
C. m ∈ (-3;-1)
D. m ∈ (1;3)
Chọn B.
Tập xác định: D = ℝ
y =
x
3
+
3
m
x
2
-
2
x
+
1
Hàm số có điểm cực đại tại x = -1 => y'(1) = 0 
Với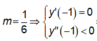 
=> Hàm số đạt cực đại tại x = -1.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
3
m
x
2
-
2
x
+
1
.
Hàm số có điểm cực đại tại x-1 khi đó giá trị của tham số m thỏa mãn A.
m
∈...
Đọc tiếp
Cho hàm số y = x 3 + 3 m x 2 - 2 x + 1 . Hàm số có điểm cực đại tại x=-1 khi đó giá trị của tham số m thỏa mãn
A. m ∈ - 1 ; 0 .
B. m ∈ 0 ; 1 .
C. m ∈ - 3 ; - 1 .
D. m ∈ 1 ; 3 .
Cho hàm số:
f
x
3
x
-
5
v
ớ
i
x
≤
-
2
m
x...
Đọc tiếp
Cho hàm số: f x = 3 x - 5 v ớ i x ≤ - 2 m x + 3 v ớ i x > - 2
Giá trị nào của m để hàm số đã cho liên tục tại x=-2?
A. 7
B. -7
C. 5
D. 1