- Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.
- Ta có : x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.
- Ta có : x = 2 nên f(2) = 2 + 1 = 3.
- Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.
- Ta có : x = -1 < 2 nên f(–1) = (-1)2 – 2 = –1.
- Ta có : x = 2 nên f(2) = 2 + 1 = 3.
Cho hàm số
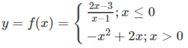
Tính giá trị của hàm số đó tại x = 5; x = -2; x = 0; x = 2
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Cho hàm số y=f(x) = ax2+ bx+c. Biểu thức f(x+ 3) -3f( x+ 2) +3f( x+ 1) có giá trị bằng.
A. ax2-bx-c.
B. ax2+ bx-c.
C. ax2- bx+ c.
D. ax2+ bx+c.
Cho hàm số \(y=f\left(x\right)=x^2+6x+5\). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y=f\left(f\left(x\right)\right)\) với \(x\in\left[-3;0\right]\). Tính tổng \(S=m+M.\)
Cho hàm số y = f ( x ) = x + 5 Giá trị của x để f(x) =2 là:
A. x= -3
B. x= -2
C.x= -7
D. Đáp án khác
Câu 35. Cho hàm số f(x) ={\(\left|\dfrac{-2\left(x-3\right)}{\sqrt{x^2}-1}\right|\) \(\dfrac{-1\le x< 1}{x\ge1}\) Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={\(\dfrac{2x+1}{x^2-3}\dfrac{khix\le2}{khix>2}\) đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={\(\dfrac{-2x+1khix\le-3}{\dfrac{x+7}{2}khix>-3}\) Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=\(\dfrac{x-2}{\left(x-2\right)\left(x-1\right)}điểm\) nào thuộc đồ thị.