Hình chóp tứ giác đều SABCD có AB = a; góc (SC, (ABCD) = 30°. Tính khoảng cách h từ điểm S đến (ABCD)
A. h = a 2 3
B. h = a 3 2
C. h = a 2 3
D. h = a 6
Hình chóp tứ giác đều S A B C D có AB = a; góc giữa (SCD) và (ABCD) bằng 60 ° . Tính diện tích xung quanh ( S x q ) của hình chóp
A. S x q = 2 a 2 2
B. S x q = a 2 3
C. S x q = 2 a 2 3
D. S x q = 2 a 2
Tính bán kính R của mặt cầu ngoại tiếp hình chóp tứ giác đều SABCD, biết A B = a , S C , A B C D ^ = 60 o .
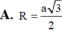
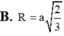
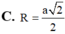
![]()
Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là một tam giác đều và nằm trong một mặt phẳng vuông góc với đáy (ABCD). Tính thể tích khối chóp SABCD.
A. a 3 6
B. a 3 3 2
C. a 3 3 6
D. a 3 2
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
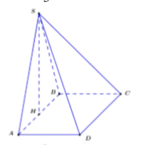
Cho hình chóp tứ giác đều SABCD có ABCD là hình vuông cạnh 20cm, cạnh bên 24cm. Tính thể tích hình chóp.
gọi O là giao điểm của AC và BD => SO vuông góc (ABCD)=>SO vuông góc AO
xét tam giác SAO có SO vuông góc AO
=>SO\(^2\)=SA\(^2\)-AO\(^2\)
=> SO=2\(\sqrt{94}\)
thể tích chóp \(\dfrac{1}{3}\).SO.s.ABCD=\(\dfrac{800}{3}\)\(\sqrt{94}\)
Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a . Gọi M là trung điểm của AD . Biết khoảng cách giữa hai đường thẳng CM và SA bằng a/căn6 . Thể tích khối chóp SABCD bằng
Cho hình chóp tứ giác SABCD có đáy là vuông; mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng ( SCD) bằng 3 7 a 7 . Tính thể tích Vcủa khối chóp SABCD
A. V = 1 3 a 3
B. V = a 3
C. V = 2 3 a 3
D. V = 3 a 3 2
Đáp án D
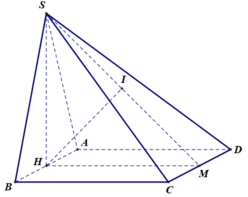
Gọi H,M lần lượt là trung điểm của AB và CD
Vì Δ S A B đều và mặt phẳng S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Ta có
C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ S H M (1)
Gọi I là hình chiếu vuông góc của H lên mặt phẳng S C D (2)
Từ (1) và (2) suy ra H I ⊥ S C D
Vì A B // C D ⇒ A B // S C D ⇒ d A , S C D = d H , S C D = H I = 3 a 7 7
Giải sử A B = x x > 0 ⇒ S H = x 3 2 H M = x .
Mặt khác: 1 H I 2 = 1 H M 2 + 1 S H 2 ⇔ 7 9 a 2 = 1 x 2 + 4 3 x 2 ⇔ x 2 = 3 a 2 ⇒ x = 3 a
Thể tích: V S . A B C D = 1 3 S H . S A B C D = 1 3 . 3 a 2 .3 a 2 = 3 a 3 2 (đvtt)
Cho hình chóp tứ giác đều S.ABCD có khoảng cách từ tâm O của đáy đến (SCD) bằng 2a, a là hằng số dương. Đặt AB=x. Giá trị của x để thể tích của khối chóp SABCD đạt giá trị nhỏ nhất là
A. a 3
B. 2 a 6
C. a 2
D. a 6
cho hình chóp tứ giác đều S ABCD có đáy ABCD là hình vuông cạnh a các mặt bên tạo với mặt đáy một góc bằng 60. tính thể tích khối chóp SABCD
Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10cm trung đoanh bằng 13cm
a) Tính độ dài cạnh bên
b) Tính diện tích xung quanh hình chóp
c) Tính thể tích hình chóp
Bạn tự vẽ hình nha
a, Gọi \(O=BD\cap AC\)
K là trung điểm của CD
\(\Rightarrow OK=\dfrac{1}{2}AD=\dfrac{1}{2}CD=5\)
b, \(S_{xq}=\left(AB+BC\right).SK\)
\(=\left(10+10\right).13\)
\(=260\left(cm^2\right)\)
c, \(V_{S_{ABCD}}=\dfrac{1}{3}.SO.SB.SC\)
\(=\dfrac{1}{3}.12.10.10\)
\(=400\left(cm^3\right)\)
-Chúc bạn học tốt-