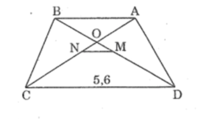
Cho hình thang cân ABCD (AB/ /CD). Hai đường chéo AC và BD cắt nhau tại O. Gọi M; N theo thứ tự là trung điểm của BD và AC. Biết MD = 3MO, đáy lớn CD = 5,6 cm.
a. Tính MN; AB?
b. So sánh MN với nửa hiệu các độ dài của CD và AB.( vẽ hình)
Những câu hỏi liên quan
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. Tính độ dài đoạn thẳng MN và đáy nhỏ AB.
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: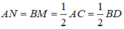 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: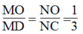 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: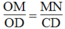 
Hệ quả định lí Ta-lét)
Suy ra: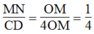 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
Đúng 0
Bình luận (0)
Hình thang cân ABCD (AB//CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3MO, đáy lớn CD = 5,6cm. So sánh độ dài đoạn thẳng MN với nửa hiệu của CD và AB
cho hình thang cân abcd có hai đáy ab song song cd gọi i là giao điểm của 2 đường chéo ac và bd đường trung trực của ad và di cắt nhau tại o chứng minh rằng oi vuông góc cới bc
cho hình thang cân abcd có hai đáy ab song song cd gọi i là giao điểm của 2 đường chéo ac và bd đường trung trực của ad và di cắt nhau tại o chứng minh rằng oi vuông góc cới bc
Cho hình thang cân ABCD có hai đáy AB// CD. Gọi I là giao điểm của 2 đường chéo AC và BD . Đường trung trực của AD và DI cắt nhau tại O. Chứng minh rằng OI vuông góc với BC.
#hinh_thang_can_ABCD
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: O M O N = A B C D
Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:
Đúng 0
Bình luận (0)
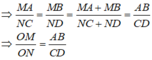
Cho hình thang ABCD (AB//CD) có 2 đường chéo AC và BD cắt nhau tại I và có IA=IB. C/m ABCD là hình thang cân
\(\Delta IAB\)cân tại I nên \(\widehat{IAB}=\widehat{IBA}\)( tính chất tam giác cân )
AB // CD (gt) \(\Rightarrow\hept{\begin{cases}\widehat{IAB}=\widehat{ICD}\\\widehat{IBA}=\widehat{IDC}\end{cases}\left(SLT\right)}\)
Do đó: \(\widehat{ICD}=\widehat{IDC}\Rightarrow\Delta ICD\)cân tại I \(\Rightarrow IC=ID\)( định nghĩa )
Ta có: \(IA+IC=IB+ID\Rightarrow AC=BD\)
Hình thang ABCD có AB // CD và 2 đường chéo AC, BD bằng nhau
Vậy ABCD là hình thang cân.
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có AB//CD, AB<CD, hai đường cheó AC và BD cắt nhau tại P , hai cạnh bên AD và BC kéo dài cắt nhau tại Q.C/M: PQ là đường trung trực của hai đáy hình thang cân ABCD
Xét ΔQDC có AB//DC
nên QA/AD=QB/BC
mà AD=BC
nên QA=QB
QA+AD=QD
QB+BC=QC
mà QA=QB và AD=BC
nên QD=QC
Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
=>ΔABD=ΔBAC
=>góc DBA=góc BAC
=>góc PAB=góc PBA
=>PA=PB
PA+PC=AC
PB+PD=BD
mà PA=PB và AC=BD
nên PC=PD
PA=PB
QA=QB
=>PQ là trung trực của AB
PD=PC
QD=QC
=>PQ là trung trực của DC
Đúng 1
Bình luận (0)
1 tháng 9 2021 lúc 12:59
Cho ABCD là hình thang cân (AB // CD) có hai đường chéo cắt nhau tại O.
a. Chứng minh: OA = OB và OC = OD
b. Chứng minh: AC + BD > AB + CD
a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{ODC}=\widehat{OCD}\)
Xét ΔOCD có \(\widehat{ODC}=\widehat{OCD}\)
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
Đúng 0
Bình luận (0)