Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
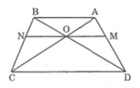
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

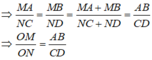
Vì OM ⊥ AB và ON ⊥ CD, mà AB // CD nên suy ra M, O, N thẳng hàng.
Mặt khác, do AB // CD nên theo Định lí Ta-lét ta có:
Từ đó, theo tính chất của dãy tỉ số bằng nhau, ta có:

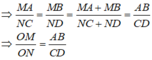
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M, K, N, H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB, BC, CD, DA. Chứng minh rằng: O H O K = B C A D
Hình tam giác ABCD ( AB// CD) có hai đường chéo AC và BD cắt nhau tại O. Gọi M,K,N,H lần lượt là chân đường vuông góc hạ từ O xuống các cạnh AB,BC,CD,DA.Chứng minh rằng:
a) OM/ON=AB/CD;
b)* OH/OK=BC/AD
Cho hình vuông ABCD tâm O, điểm M nằm trên đường chéo AC (M khác với A, C). Gọi H, K, P và Q lần lượt là chân đường vuông góc hạ từ M xuống CD, AD, BC và AB.
1) Chứng minh các tứ giác MHCP, MQAK là các hình vuông.
2) Chứng minh rằng tam giác KAB = tam giác HDA và BK vuông gióc với AH.
Giúp mình với ạ. Mình cảm ơn trước
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng d1 qua O cắt cạnh AB và CD lần lượt tại M và P , đường thẳng d2 qua O cắt cạnh BC và DA lần lượt tại N và Q . Biết d1 vuông góc với d2 . Chứng minh :
a/ Tứ giác MNPQ là hbh
b/ Từ giác MNPD là hình thoi
Cho hình thang ABCD (AB//CD) có CD = 2AB. Gọi O là giao điểm của hai đường chéo AC và BD, F là giao điểm cạnh bên AD và BC
a) Chứng minh OC = 2OA
b) Điểm O là điểm đặc biệt gì trong tam giác FCD
c) Một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD, AC, BC tại M, I, K, N. Chứng minh DM/AD=CN/BC
Bài 9: Cho hình bình hành ABCD. Hai đường chéo AC,BD cắt nhau tại O. Đường m đi qua O cắt AB,CD lần lượt tại M,P. Đường thẳng n đi qua O và vuông góc với m cắt BC và DA lần lượt tại N,Q.
Cm MNPQ là hình bình hành
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O vuông góc với AB và CD lần lượt tại H và K. Chứng minh OH/OK = AB/CD
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.