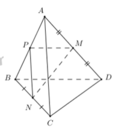
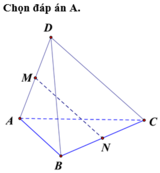
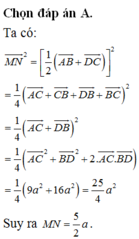Cho tứ giác ABCD có AD = BC. Gọi M,N lần lượt là trung điểm của AC và BD; MN cắt AD, BC lần lượt tại I,K. CMR góc AIM = góc BKN

Những câu hỏi liên quan
Cho tứ giác abcd có AC=BD. Gọi M và N lần lượt là trung điểm của AD, BC. H và G lần lượt là giao điểm của MN với 2 đường chéo AC và BD Chứng minh: góc AHM bằng góc BGN
Cho tứ giác ABCD. Gọi E và F lần lượt là trung điểm của AD và BC. Đường thẳng EF cắt AC và BD lần lượt tại M và N. Biết rằng góc AME=BNF. CMR AC=BD
Cho tứ giác ABCD gọi M, N lần lượt là trung điểm của AD, BC. H và G lần lượt là giao của MN với AC và BD. CMR: AC=BD khi và chỉ khi góc AHM = góc BGN
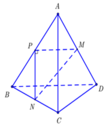
Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP PN . Chọn câu đúng.A.overrightarrow{AC} overrightarrow{BD} B.overrightarrow{AC} overrightarrow{BC} C. overrightarrow{AD} overrightarrow{BC} D. overrightarrow{AD} overrightarrow{BD}
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP PN . Chọn câu đúng.
A.\(\overrightarrow{AC}\) = \(\overrightarrow{BD}\)
B.\(\overrightarrow{AC}\) = \(\overrightarrow{BC}\)
C. \(\overrightarrow{AD}\)= \(\overrightarrow{BC}\)
D. \(\overrightarrow{AD}\)= \(\overrightarrow{BD}\)
Cho tứ giác ABCD gọi M,N lần lượt là trung điểm của AD, BC. H và G lần lượt là giao của MN với AC và BD. CMR: AC=BD khi và chỉ khi góc AHM= góc BGN
Cho tứ diện ABCD có AC 3a,
B
D
4
a
. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
Đọc tiếp
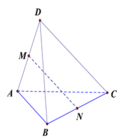
Cho tứ diện ABCD có AC = 3a, B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
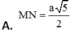
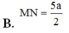
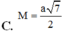
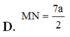
Cho tứ diện ABCD có
A
C
3
a
,
B
D
4
a
. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.
Đọc tiếp
Cho tứ diện ABCD có A C = 3 a , B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.
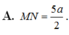
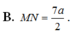
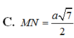

Cho tứ diện ABCD có AC3a, BD4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN A.
M
N
5
a
2
B.
M
N
7
a
2
C.
M
N
7
a
2
D.
M
N...
Đọc tiếp
Cho tứ diện ABCD có AC=3a, BD=4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
A. M N = 5 a 2
B. M N = 7 a 2
C. M N = 7 a 2
D. M N = 5 a 2
Cho tứ diện ABCD có AC 3a, BD 4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN A.
M
N
a
5
2
B.
M
N
5
a
2
C.
M
N
a
7
2
D. ...
Đọc tiếp
Cho tứ diện ABCD có AC = 3a, BD = 4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
A. M N = a 5 2
B. M N = 5 a 2
C. M N = a 7 2
D. M N = 7 a 2
Phương pháp
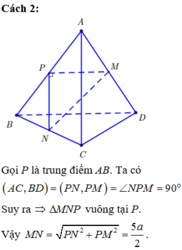
+) Gọi P là trung điểm của AB. Chứng minh tam giác MNP vuông tại P.
+) Áp dụng định lý Pytago trong tam giác vuông MNP tính MN.
Cách giải

Đúng 0
Bình luận (0)