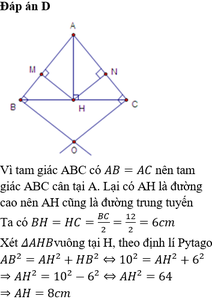
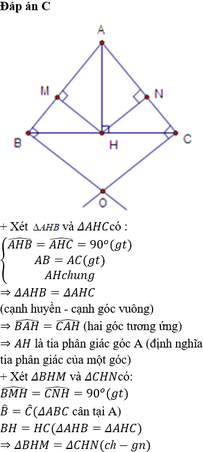
1. Cho ∆ABC có AB < AC. Vẽ AH vuông góc BC (H∈BC); HI vuông góc AC tại I. Trên tia đối của tia IH lấy điểm E sao cho IE = HI. C/m:
a/ AE vuông góc CE. b/ góc BAH < CAH.
2. Cho ∆ABC vuông tại A. Trên cạnh AC lấy các điểm D và E sao cho AD = DE = EC. So sánh gióc ABD và góc DBE.
---> Giúp e giải hai bài trên với ạ... T︵T