Cho tam giác DEF, I là trung điểm cua EF. Từ E và F kẻ EH⊥DI tại H; FK⊥DI tại K.
a) Chứng minh: IH=IK.
b) Chứng minh: DE+DF>DH+DK.
c) Chứng minh: DH+DK=2DI.
d) Chứng minh: DE+DF>2DI.
Những câu hỏi liên quan
Câu5: (3,5 điểm) Cho tam giác DEF cần tại D. Kẻ D1 perp EF tại I. a) Chứng minh: Delta*D * I * E = Delta*D * I * F và I là trung điểm của EF. c) Từ I kẻ IA L DE tại A, IB perp DF . Gọi H là giao điểm của IB và DE, K là giao điểm của IA và DF. Chứng minh: ADHK cân và hat HDK =180^ -2 hat DHK d) Gọi G là trung điểm HK. Chứng minh: Ba điểm Dạ I, G thẳng hàng.
Cho tam giác DEF vuông tại E có ED EF. Kẻ EH vuông góc với DFa) So sánh DH và HF ?b) Giả sử góc EDF 60 độ . I là điểm thuộc đoạn thẳng DF sao cho EDDI. Tam giác EDI là tam giác gì? Vì sao?c) Vẽ trung tuyến FA. Trên tia đối của tia AF lấy điểm B sao cho AB AF . Chứng minh BD vuông góc với DE .d) Gọi G là trọng tâm của tam giác BDF . Biết GA 3cm. Tính DE .e) Gọi K là điểm nằm trên đoạn thẳng EA sao cho EKdfrac{2}{3} AE, FK cắt BE tại M , N là giao điểm của BF và DM . Chứng minh: BF 3 BN
Đọc tiếp
Cho tam giác DEF vuông tại E có ED <EF. Kẻ EH vuông góc với DF
a) So sánh DH và HF ?
b) Giả sử góc EDF = 60 độ . I là điểm thuộc đoạn thẳng DF sao cho ED=DI. Tam giác EDI là tam giác gì? Vì sao?
c) Vẽ trung tuyến FA. Trên tia đối của tia AF lấy điểm B sao cho AB =AF . Chứng minh BD vuông góc với DE .
d) Gọi G là trọng tâm của tam giác BDF . Biết GA = 3cm. Tính DE .
e) Gọi K là điểm nằm trên đoạn thẳng EA sao cho EK=\(\dfrac{2}{3}\) AE, FK cắt BE tại M , N là giao điểm của BF và DM . Chứng minh: BF =3 BN
a: ED<EF
=>HD<HF
b: Xét ΔDEI có DE=DI và góc D=60 độ
nên ΔDEI đều
c: Xét tứ giác FEBD có
A là trung điểm chung của FB và ED
=>FEBD là hbh
=>FE//BD
=>BD vuông góc DE
Đúng 0
Bình luận (0)
Cho tam giác DEF vuông tại D, phân giác EB. Kẻ BI vuông góc với EF tại I. Goi H la giao diem cua ED va IB. CM:a) Tam giác EDB=EIB.b)HB=BFc)Gọi K là trung điểm của HF. . CM: E,B,K thẳng hàng d. DI//HF
cho tam giac DEF cân tại D.trên cạnh DE,DF lấy K;H sao cho DK=dh.gọi i là giao điểm của eh và fk.chứng minh a,tam giác ìe cân tại i b,i cách đều 2 cạnh de và df c,di đi qua trung điểm của ef và vuông góc với ef
Cho tam giác DEF có DE=5cm, DF=9cm, DI là đường phân giác ( I thuộc EF ). Kẻ EM, FN vuông góc với DI. Qua trung điểm K của EF kẻ đường thẳng song song với DI cắt DF tại H, cắt ED tại C. Chứng minh EC=FH.
Xem chi tiết
???????????????????????????????????????????????????
Xem thêm câu trả lời
Cho tam giác DEF vuông tại D, EK là tia phân giác của góc DEF ( K thuộc DF ). Trên tia EF lấy điểm H sao cho EH=ED.
a) Chứng minh tam giác EDK=tam giác EHK, từ đó chứng minh HK vuông góc với EF
b) Từ H kẻ đường thẳng vuông góc với DF, nó cắt DF tại I. Chứng minh HI // ED
Cho tam giác DEF vuông tại E (DE<EF) đường cao EH. Kẻ HI vuông góc ED ( I thuộc ED ), HK vuông góc EF ( K thuộc EF )
a) c/m EIHK là hình chữ nhật
b) Gọi O là trung điểm của HE. C/m I,O,K thẳng hàng
c) Kẻ trung tuyến EN cắt IK tại M. Tính số đo góc EMK
Cho tam giác DEF cân tại E, kẻ EH là phân giác E ( H thuộc DF )
a) Chứng minh tam giác EHD = tam giác EHF
b) Từ H, kẻ HP vuông góc với DE ( P thuộc DF ), HM vuông góc EF ( M thuộc EF )
c) Biết DE = 5cm, DF = 6cm, Tính EH
Vẽ hình giúp mình
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
Đúng 0
Bình luận (0)
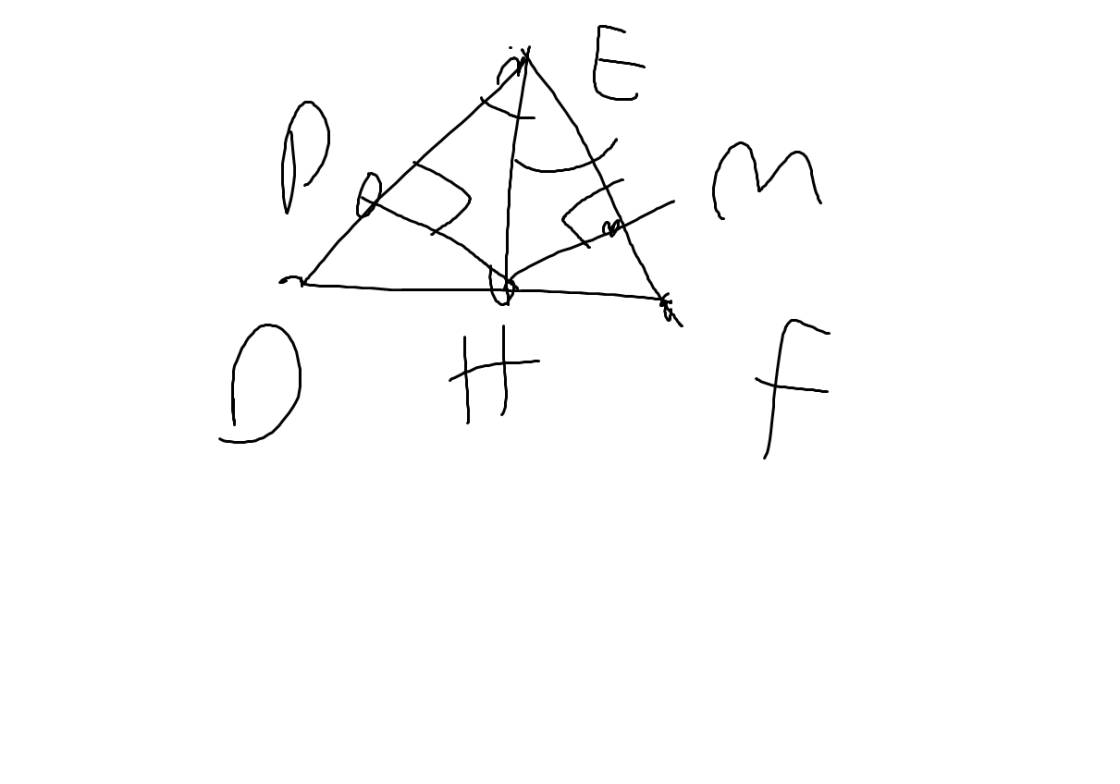
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) Chứng Minh tam giác DEI = tam giác DEF
b)Các góc DIE và góc DÌ là những góc gì
c)Biết DI=12cm;EF=10cm . Hãy tính độ dài cạnh DE
d)Từ E và F kẻ các đường thẳng vuông góc với ED và FD chúng cắt nhau tại M
Chứng Minh ; D,I,M thẳng hàng