Cho tứ giác ABCD có \(F\in AC\) . Kẻ FE // CD (\(E\in AD\)); FG // BC (\(G\in AB\)). CM:
\(AF.BG=DE.AG\)
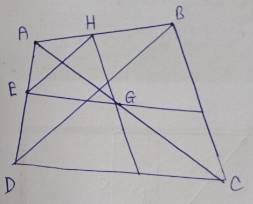
Cho tứ giác ABCD có E thuộc cạnh AD. Kẻ EG // CD (G in AC ) và kẻ GH // BC (H in AB a. Chứng minh: HE // BD. b. Chứng minh: AE .BH=AH.DE.
a: GE//CD
=>AG/AC=AE/AD
GH//BC
=>AG/AC=AH/AB
=>AE/AD=AH/AB
=>EH//BD
b: Vì EH//BD
nên AE/ED=AH/HB
=>AE*HB=AH*DE
a) Ta có: HG // BC (gt).
\(\Rightarrow\dfrac{AH}{HB}=\dfrac{AG}{AC}\) (1) (Định lý Ta - let).
Ta có: GE // CD (gt).
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AG}{AC}\) (2) (Định lý Ta - let).
Từ (1) và (2) \(\Rightarrow\dfrac{AE}{AD}=\dfrac{AH}{AB}.\)
\(\Rightarrow\) HE // BD.
b) Ta có: HE // BD (cmt).
\(\Rightarrow\dfrac{AE}{DE}=\dfrac{AH}{BH}\) (Định lý Ta - let).
\(\Rightarrow AE.BH=AH.DE\left(đpcm\right).\)
Cho tứ giác ABCD cỏ E thuộc cạnh AD. Kẻ EG // CD (G in AC ) và kẻ GH // BC (H in AB a. Chứng minh: HE // BD. b. Chứng minh: AE .BH=AH.DE.
Các bước giải:
a) Vì EG // CD nên theo định lí Thalet ta có: \(\dfrac{AE}{AD}\) = \(\dfrac{AG}{AC}\)
Vì GH // CB nên theo định lí Thalet ta có: \(\dfrac{AG}{AC}\)= \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AG}{AC}\) = \(\dfrac{AH}{AB}\) ⇒ HE // BD (đpcm) (Thalet đảo)
b) HE // BD ⇒ \(\dfrac{AE}{AD}\) = \(\dfrac{AH}{AB}\)
⇒ \(\dfrac{AE}{AD-AE}\) = \(\dfrac{AH}{AB-AH}\)
⇒ \(\dfrac{AE}{DE}\) = \(\dfrac{AH}{BH}\)
⇒\(AE.BH=AH.DE\left(đpcm\right)\)

Các bước giải:
a) Vì EG // CD nên theo định lí Thalet ta có: \(\dfrac{AG}{AC}\)
Vì GH // CB nên theo định lí Thalet ta có: \(\dfrac{AG}{AC}\) = \(\dfrac{AE}{DE}\) = \(\dfrac{AH}{BH}\)
⇒ AE.BH = AH.DE
Cho tứ giác ABCD có điểm E thuộc AC,Kẻ EF//AB,F thuộc BC. Kẻ EI//CD,I thuộc AD .Chứng minh EF/AB+EI/CD=1
THeo thales ta có
\(\Rightarrow\hept{\begin{cases}\frac{EF}{AB}=\frac{CE}{CA}\\\frac{EI}{CD}=\frac{AE}{AC}\end{cases}\Rightarrow}\frac{EF}{AB}+\frac{EI}{CD}=\frac{CE}{CA}+\frac{AE}{AC}=1\)VẬY ta có đpcm
cho tứ giác abcd e thuộc ac. kẻ ef//ab (f thuộc bc) ei//cd ( i thuộc ad) chứng minh ef/ab + ei/cd = 1
Bài 1: Cho tứ giác ABCD, E là trung điểm cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F. Qua F kẻ đường thẳng song song với BD cắt CD ở G. Qua G kẻ đường thẳng song song với AC cắt AD ở H.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Tứ giác ABCD cần thêm điều kiện gì để tứ giác EFGH là hình chữ nhật.
Các bạn giúp mình nhé, mình đang cần gấp. Cảm ơn các bạn nhiều.
Xét tg ABC có
EF//AC (gt) (1)
EA=EB (gt)
=> FB=FC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và song song với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
EA=EB (gt); FB=FC (cmt) => EF là đường trung bình của tg ABC
\(\Rightarrow EF=\dfrac{1}{2}AC\) (2)
Xét tg BCD chứng minh tương tự ta cũng có GC=GD
Xét tg ADC có
GF//AC (gt) (3)
GC=GD (cmt)
=> HA=HD (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và song song với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
GC=GD (cmt); HA=HD (cmt) => GH là đường trung bình của tg ADC
\(\Rightarrow GH=\dfrac{1}{2}AC\) (4)
Từ (1) và (3) => EF//GH (cùng // với AC)
Từ (2) và (4) \(\Rightarrow EF=GH=\dfrac{1}{2}AC\)
=> EFGH là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
b/
Gọi O là giao của AC và BD
Ta có
FG//BD (gt); GH//AC (gt) \(\Rightarrow\widehat{HGF}=\widehat{DOC}\) (Góc có cạnh tương ứng vuông góc)
Để EFGH là Hình chữ nhật \(\Rightarrow\widehat{HGF}=90^o\)
\(\Rightarrow\widehat{HGF}=\widehat{DOC}=90^o\Rightarrow AC\perp BD\)
Để EFGH là hình chữ nhật => ABCD phải có 2 đường chéo vuông góc với nhau
Cho tứ giác ABCD có ∠A= ∠ C=90· . Từ điểm M trên BD,kẻ ME⊥AD ở E,MF⊥CD ở F . chứng minh EF//AC
Cho hình bình hành ABCD có AB > AD . qua A kẻ đg thg vuông BD tại E , cắt CD tại I . qua CK kẻ đg thg vuông BD tại F , cắt AC tại K.
a, CM : tứ giác AECI là hình gì vì sao
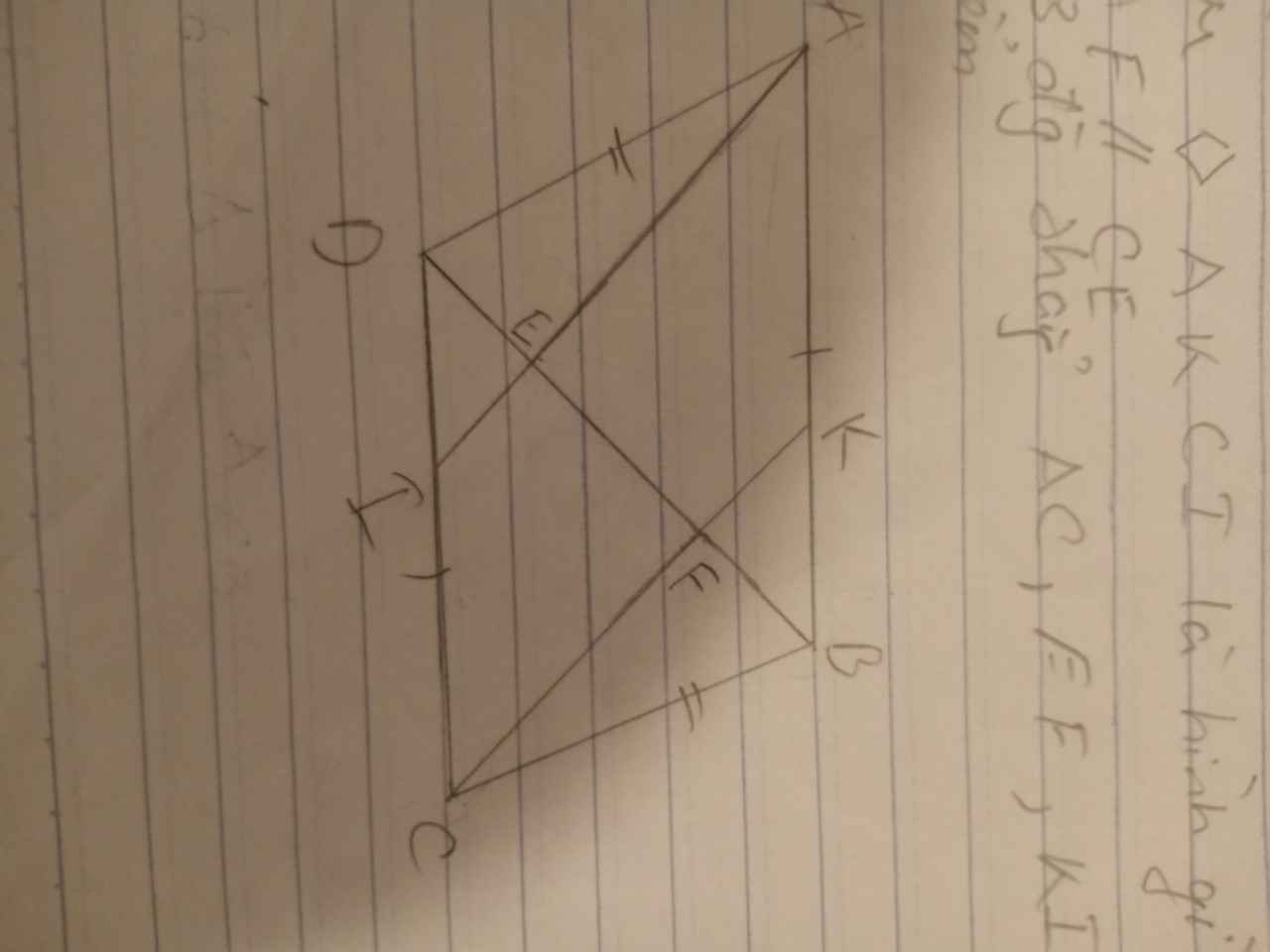
cho tứ giác abcd có ac vuông góc bd. gọi e,f là trung điểm của ab và ad. kẻ eh vuông góc cd tại h,fk vuông góc bc tại k cm ac,eh,fk là đồng quy
Cho tứ giác ABCD,Ethuộc AB.Qua E kẻ đường thẳng song song với AC cắt BC ở F .Qua F kẻ đường thẳng song song vớiBD cắt CD ở G.Qua G kẻ đường thẳng song song với AC cắt AD tại H.
a)Xác định dạng tứ giác EFGH
b)Cho EFGH là hình chứ nhật .TínhSABCD và SEFGH