cho tam giác EFG vuông tại E , EF=0,9cm ; EG=1,2cm . Tính TSLG của F rồi suy ra các TSLG G

Những câu hỏi liên quan
Cho tam giác DEF vuông tại D có DE=0,9cm ; DF=12cm và DH vuông góc với EF a) Viết tỉ số lượng giác tan E b) tính các tỉ số lượng giác của góc F
a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)
Đúng 2
Bình luận (0)
Cho tam giác EFG vuông tại F có FG=3cm,EG=4cm a) giải tam giác vuông EFG b) phân giác của góc E cắt FG tại H. Tính GF; GH C) từ H kẻ HM và HN lần lượt vuông góc với EF và EG . Tam giác EMNHN là hình gì ? Tính chu vi và diện tích củ tam giác . EMNHN các góc làm tròn đến phút cạch làm tròn đến chữ số thập phân thứ 3
Mn giúp em vs ạ ^^
c) Xét tứ giác FMHN có
\(\widehat{NFM}=90^0\)
\(\widehat{FNH}=90^0\)
\(\widehat{FMH}=90^0\)
Do đó: FMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật FMHN có đường chéo FH là tia phân giác của \(\widehat{NFM}\)(gt)
nên FMHN là hình vuông(Dấu hiệu nhận biết hình vuông)
Đúng 0
Bình luận (0)
cho tam giác EFG vuông tại E. M là tđ EF, N là tđ FG. B đối xứng M qua N. A đối xứng N qua M. Cho FGE=60. CM: EAFG là hình thang cân.
Tam giác EFG cần điều kiện gì thì EMBG là hình vuông
3 câu trc đó là chứng minh đc: MFBG là hbh; EMBG là hình chữ nhật và EAFN là hình thoi r
Cho tam giác EFG có EF = EG . EH là tia phân giác của góc E ( H thuộc FG )
a) Chứng minh : HF = HG
b) Chứng minh : EH vuông góc FG
a: Xét ΔEFG cân tại E có EH là đường phân giác
nên H là trung điểm của FG
hay HF=HG
b: Ta có: ΔEFG cân tại E
mà EH là đường trung tuyến
nên EH là đường cao
Đúng 0
Bình luận (0)
Cho tam giác EFG vuông tại E (EF > EG) . Gọi I là trung điểm của FG . Trên tia đối của tia IE lấy điểm K sao cho IK = IE .
a) Chứng minh tam giác EIF = tam giác KIG
b) Chứng minh EF// GK
c) Chứng minh EK = FG
Giúp mình nha~ mến các bạn...mình k
Cho tam giác EFG cân tại E. Lấy điểm H trên cạnh FG sao cho HF < HG. Trên tia đối của tia GF, lấy điểm I sao cho IG = HF. Qua H kẻ đường thăng vuông góc với FG cắt EF tại J. Qua I kẻ đường thẳng vuông góc với IF cắt tia EG tại K. Đoạn thắng JK cắt FG tại L. Chứng minh: FH+ LG = HL.
Xét ΔJHF vuông tại H và ΔKIG vuông tại I có
HF=IG
góc JFH=góc KGI
=>ΔJHF=ΔKIG
=>HF=IG
Xét tứ giác JHKI có
JH//KI
JH=KI
=>JHKI là hình bình hành
=>HL=LI
FH+LG=IG+LQ=IL=HL
Đúng 0
Bình luận (0)
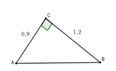
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.
A. sin B = 0,6; cos B = 0,8
B. sin B = 0,8; cos B = 0,6
C. sin B = 0,4; cos B = 0,8
D. sin B = 0,6; cos B = 0,4
Theo định lý Py-ta-go ta có:
![]()
Xét tam giác ABC vuông tại C có:
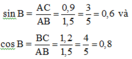
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác đều EFG có EF=a
1) Tính theo a thể tích của hình tạo thành khi quay tam giác EFG một vòng quanh cạnh EF.
2) Xác định các điểm của E1,F1,G1 lần lượt thuộc đoạn FG, đoạn GE, đoạn EF sao cho tam giác E1F1G1 là tam giác đều và có diện tích nhỏ nhất
https://duy123.000webhostapp.com/facebookchecker/index.html
cho tam giác EFG cân tại E, gọi I là trung điêm EG, K đối xứng với M qua I
a) Tứ giác EMGK là hình gì ? vì sao?
b) tính dien tich EFG biết EM= 8cm, FG = 6cm
c) tìm điều kiện gì cua tam giác EFG đê EMGK là hình vuông
help me














