Cho tứ diện ABCD có ABCD và D A ⊥ A B C ; DA = 1 là tam giác đều cạnh bằng 1. Trên ba cạnh DA, DB, DC lấy 3 điểm M, N, P mà D M D A = 1 2 ; D N D B = 1 3 ; D P D C = 3 4 Tính thể tích khối tứ diện MNPD
A. V = 3 12
B. V = 2 12
C. V = 3 96
D. V = 2 96
Tứ diện ABCD. Các điểm A'B'C'D' là điểm chia AB, BC, CD, DA theo tỉ số k (k≠1). Chứng minh tứ diện ABCD và tứ diện A'B'C'D' có cùng trọng tâm
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Chọn đáp án C.
Ta có
![]()
![]()
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:
A. 1/2 B. 1/4
C. 1/6 D. 1/8.
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
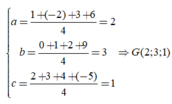
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
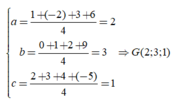
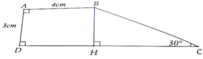
Cho tứ giác ABCD có B ^ = D ^ = 90 0 , C ^ = 30 0 , AB=4cm và AD = 3cm. Tính diện tích tứ giác ABCD
Kẻ BH ⊥ DC tại H. Chú ý diện tích ABCD bằng tổng diện tích của ABHD và BHC
Cho hai mặt cầu ( S 1 ) v à ( S 2 ) đồng tâm I, có bán kính lần lượt là R 1 = 2 v à R 2 = 10 . Xét tứ diện ABCD có hai đỉnh A , B nằm trên ( S 1 ) và hai đỉnh C , D nằm trên ( S 2 ) . Thể tích lớn nhất của khối tứ diện ABCD bằng
![]()
![]()
![]()
![]()
cho tứ giác ABCD nối A với C trên AC lấy E sao cho CE = 1/3 AC. Nối E với B và D biết diện tích tứ giác ABED là 45 cm2. tính diện tích tứ giác ABCD
Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với A(3;5;-1),B(0;-1;8),C(-1;-7;3),D(1;0;2) và điểm M(1;1;5). Mặt phẳng (P):ax+by+cz-14=0 qua hai điểm D,M cắt cạnh AC và (P) chia khối tứ diện ABCD thành hai phần có thể tích bằng nhau. Giá trị của biểu thức a+b+c bằng
A. 10
B. 16
C. 8
D. -36
Cho tứ giác ABCD có AC = BD và AC vuông góc BD. khi đó : A. Tứ giác ABCD là hình vuông B. Tứ giác ABCD là hình bình hành C. Tứ giác ABCD là hình thoi D. ABCD là tứ giác bất kì