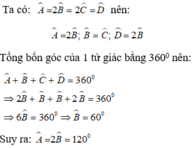Cho tứ giác ABCD có A=2B, B=2C; C=3D. Tính góc D

Những câu hỏi liên quan
Cho tứ giác ABCD có A=2B,B=2c,C=2D.tính các góc của tứ giác
B=2*C=2*2D=4*D
A=2*B=2*4D=8*D
Xét tứ giác ABCD có
góc A+góc B+góc C+góc D=360 độ
=>8*góc D+4*góc D+2*góc D+góc D=360 độ
=>góc D=24 độ
góc C=2*24=48 độ
góc B=4*24=96 độ
góc A=8*24=192 độ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có
A
^
2
B
^
2
C
^
D
^
. Tính số đo góc A? A.
105
o
B.
100
o
C.
120
o
D.
75
o
Đọc tiếp
Cho tứ giác ABCD có A ^ = 2 B ^ = 2 C ^ = D ^ . Tính số đo góc A?
A. 105 o
B. 100 o
C. 120 o
D. 75 o
Tứ giác ABCD có góc A=2B=2C=4D, tính góc A
Giải giúp em gấp với ạ
Áp dụng tc dstbn:
\(\widehat{A}=2\widehat{B}=2\widehat{C}=4\widehat{D}\Rightarrow\dfrac{\widehat{A}}{4}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{2}=\dfrac{\widehat{D}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{4+2+2+1}=\dfrac{360^0}{9}=40^0\\ \Rightarrow\widehat{A}=40^0\cdot4=160^0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tứ giác ABCD tính các góc của tứ giác trong các trường hợp sau:
a.góc A=150 B=3C C=2D
b.A=2B C+D=210
c.A=2B=3C=4D
dd.A=1/2B B=2C C=D
a) Xét tứ giác ABCD ta có ( ^B = 2^C mới được nhé)
^A + ^B + ^C + ^D = 3600
=> 1500 + ^B + ^C + ^D = 3600
=> ^B + ^C + ^D = 2100
Có ^B = 2^C
=> 2 ^C + ^C + ^D = 2100
=> 3^C + ^D = 2100
Có ^C = 2^D
=> 3 . 2^D + ^D = 2100
=> 7^D = 2100
=> ^D = 300
+) ^C = 2^D = 2.300 = 600
+) ^B = 2^C = 2.600 = 1200
b) Xét tứ giác ABCD có :
^A + ^B + (^C + ^D) = 3600
=> 2^B + ^B + 2100 = 3600
=> 3^B = 1500
=> ^B = 500
+) ^A = 2^B = 2.500 = 1000
Có ^C + ^D = 2100 => ^C = ^D = 210 : 2 = 1050
Vậy ^A = 1000,^B = 500,^C = ^D = 1050
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)
=> ^A = 360 , ^B = 720 , ^C = 1080 , ^D = 1440
d) Tự làm
tứ giác ABCD cóA=2B=2C=4D. Số đo góc B bằng:
A.160 B.40 C.120 D.80
Xem thêm câu trả lời
Cho tứ giác ABCD có A = 2B, B = 2D, C = 3/2D. Tính số đo mỗi góc của tứ giác ABCD.
a) hình thang ABCD (AB//CD) có A - D = 20 độ , B=2C. Tính các góc trong hình thang
b) cho tứ giác ABCD có AB=BC và AC là phân giác của góc A . Chứng minh tứ giác ABCD là phân giác
a) hình thang ABCD (AB//CD) có A - D = 20 độ , B=2C. Tính các góc trong hình thang
b) cho tứ giác ABCD có AB=BC và AC là phân giác của góc A . Chứng minh tứ giác ABCD là phân giác
cho tứ giác ABCD có góc A = 30 góc B = 2C (AB//CD) tính góc b,c,d
Ta có: Vì AB // CD
=> \(\widehat{D}=180^0-\widehat{A}=180^0-30^0=150^0\)
Vì \(\widehat{B}+\widehat{C}=180^0\Leftrightarrow2\widehat{C}+\widehat{C}=180^0\Leftrightarrow3\widehat{C}=180^0\)
\(\Rightarrow\widehat{C}=60^0\Rightarrow\widehat{B}=120^0\)
Cho tứ giác ABCD có A=2B=3C=4D TÍNH D
Xem chi tiết
Ta có: \(\left\{{}\begin{matrix}2\widehat{B}=4\widehat{D}\\3\widehat{C}=4\widehat{D}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=2\widehat{D}\\\widehat{C}=\dfrac{4}{3}\widehat{D}\end{matrix}\right.\)
Tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Rightarrow4\widehat{D}+2\widehat{D}+\dfrac{4}{3}\widehat{D}+\widehat{D}=360^0\)
\(\Rightarrow\widehat{D}\left(4+2+\dfrac{4}{3}+1\right)=360^0\)
\(\Rightarrow\widehat{D}.\dfrac{25}{3}=360^0\)
\(\Rightarrow\widehat{D}=360^0:\dfrac{25}{3}=43,2^0\)
Đúng 2
Bình luận (0)
\(TC:\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
\(\Rightarrow\widehat{A}+\dfrac{1}{2}\widehat{A}+\dfrac{1}{3}\widehat{A}+\dfrac{1}{4}\widehat{A}=360^0\)
\(\Rightarrow\widehat{A}=172.8^0\)
\(\widehat{D}=\dfrac{1}{4}\widehat{A}=\dfrac{1}{4}\cdot172.8=43.2^0\)
Đúng 2
Bình luận (0)