Cho 3 điểm A(0;3) B(1;-1) C(-1;-5) Chứng tỏ rằng A; B; C thẳng hàng
Giúp mik vs =)) ![]()
Cho các điểm A(-1; 0), B(0; 2), C(2; -3), D(3; 0), O(0; 0). Có bao nhiêu điểm nằm trên trục hoành trong số các điểm trên?
A. 0
B. 1
C. 2
D. 3
Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D
Cho điểm A (0,-3) và đường thẳng d:2x-y-3=0 . Tìm điểm K trên Ox sao cho d(A:d)=d(K:d)
Thay tọa độ A vào (d) thỏa mãn \(\Rightarrow A\in d\Rightarrow d\left(A;d\right)=0\)
\(\Rightarrow d\left(K;d\right)=0\Rightarrow K\in d\)
\(\Rightarrow K\) là giao điểm của d và trục Ox
Tọa độ K là nghiệm: \(\left\{{}\begin{matrix}y=0\\2x-y-3=0\end{matrix}\right.\)
\(\Rightarrow K\left(\dfrac{3}{2};0\right)\)
Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Cho A( 0; 3) ; B(4;2)Điểm D thỏa
O D → + 2 D A → - 2 D B → = 0 → , tọa độ điểm D là:
A.(2; 8)
B. (4; -8)
C.( 8; -2)
D.đáp án khác
Cho A( 0; 3) ; B( 4; 2) . Điểm D thỏa O D → + 2 D A → - 2 D B → = 0 → ,tọa độ điểm D là:
A. (2; 8)
B. (4; -8)
C. ( 8; -2)
D. đáp án khác
Cho 3 điểm A (0; 3); B (2; 2); C (m + 3; m). Giá trị của điểm m để 3 điểm A, B, C thẳng hàng là?
A. 1
B. −3
C. 3
D. −1
Gọi d: y = ax + b là đường thẳng đi qua A và B
A ( 0 ; 3 ) ∈ ( d ) ⇔ a . 0 + b = 3 ⇔ b = 3 B ( 2 ; 2 ) ∈ ( d ) ⇔ a . 2 + b = 2 ⇒ b = 3 2 a + b = 2 ⇔ b = 3 a = − 1 2 ⇒ d : y = − 1 2 x + 3
Để 2 điểm A, B, C thẳng hàng thì C ( m + 3 ; m ) ∈ ( d ) y = − 1 2 x + 3
⇔ m = − 1 2 ( m + 3 ) + 3 ⇔ 3 2 m = 3 2 ⇒ m = 1
Vậy m = 1
Đáp án cần chọn là: A
Trên mp tọa độ Oxy cho 3 điểm A(a;0); B(0;b) (a>0; b>0) và C(1;2)
a/viết pt đường thẳng đi qua 2 điểm A, B
b/tìm hệ thức liên hệ giữa a, b sao ho 3 điểm A, B, C thẳng hàng
c/tìm các giá trị của a, b sao cho 3 điểm A, B, C thẳng hàng và SOAB nhỏ nhất
a) gọi đường thẳng đi qua \(A;B\) có dạng : \(\left(d\right):y=cx+d\)
vì \(A;B\in\left(d\right)\) \(\Rightarrow\left\{{}\begin{matrix}ac+d=0\\d=b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}d=b\\c=\dfrac{-d}{a}=\dfrac{b}{a}\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=\dfrac{b}{a}x+b\)
b) để \(A;B;C\) thẳng hàng \(\Leftrightarrow C\in\left(d\right)\)
\(\Leftrightarrow\dfrac{b}{a}+b=2\Leftrightarrow b\left(\dfrac{1}{a}+1\right)=2\)
c) từ \(b\left(\dfrac{1}{a}+1\right)=2\Leftrightarrow b=\dfrac{2a}{a+1}\)
ta có : \(A\in Ox\) và \(B\in Oy\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\sqrt{a^2}\sqrt{b^2}=\dfrac{1}{2}ab=\dfrac{1}{2}a\dfrac{2a}{a+1}\)
\(=\dfrac{a^2}{a+1}=S\)
\(\Leftrightarrow a^2-Sa-S=0\) phương trình này luôn có nghiệm \(\Rightarrow\Delta\ge0\)
\(\Leftrightarrow S^2+4S\ge0\Leftrightarrow S\left(S+4\right)\ge0\Leftrightarrow S\ge0\)
dấu "=" xảy ra khi \(a=0\) ; \(b=0\)
saint suppapong udomkaewkanjana ĐP Nhược Giang Nguyễn Thanh Hằng Ngô Kim Tuyền Ngô Thành Chung Mysterious Person Mashiro Shiina Fa Châu De DDTank JakiNatsumi
Cho hai bộ ba điểm: A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1). Hỏi bộ nào có ba điểm thẳng hàng?
Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó 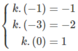
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
(d):y=mx-3 `(m \ne 0)`. Gọi `A` là giao điểm của (d) với Oy. Tìm tọa độ điểm A <Đáp án: A(0;-3)>. tìm tất cả `m` để (d) cắt trục Ox tại điểm B sao cho OA=2OB
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\mx-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{m}\\y=0\end{matrix}\right.\)
=>B(3/m;0)
\(OB=\sqrt{\left(\dfrac{3}{m}-0\right)^2+\left(0-0\right)^2}=\sqrt{\dfrac{9}{m^2}}=\dfrac{3}{\left|m\right|}\)
\(OA=\sqrt{\left(0-0\right)^2+\left(-3-0\right)^2}=3\)
OA=2OB
=>\(3=\dfrac{6}{\left|m\right|}\)
=>|m|=6/3=2
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)