cho tam giác ABC cân tại A các đường cao AE ; BK cắt nhau tại H .Chứng minh AE = BK; AH vuông góc với BC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, trực tâm H của tam giác chia đường cao AE theo tỉ số 7:1. Giao điểm I của các đường phân giác của tam giác ABC chia AE theo tỉ số nào?
Cho tam giác ABC cân tại A, trực tâm H của tam giác chia đường cao AE theo tỉ số 7:1. Giao điểm I của các đường phân giác của tam giác ABC chia AE theo tỉ số nào?
Bài 1. Cho tam giác ABC cân tại A, đường cao AD, phân giác của góc B cắt AC tại E sao cho AE
= 2 AD. Tính các góc của tam giác ABC?
Cho tam giác ABC cân tại A. Vẽ D sao cho A là trung điểm của BD. Kẻ đường cao AE của tam giác ABC, đường cao AF của tam giác ACD. Chứng minh rằng góc EAF=90 độ
Cho tam giác ABC cân tại A, đường cao AE. Lấy điểm D sao cho A là trung điểm của BD. Qua A vẽ đường thẳng song song với BC cắt DC tại H.
a, AE// DC
b, tam giác DA = tam giác ABH
Do tam giác ABC cân tại A nên AB=AC
ta thấy A là trung điểm của BD nên AB=AD
từ đó ta có được AC=AB=AD
Xét tam giác BCD có AC=AD=AB (CA là trung tuyến của cạnh BD)
nên tam giác BCD vuông tại C tức CD vuông góc với BC
Tam giác ABC cân tại A ,AE là đường cao nên AE vuông góc với BC
từ đây suy ra AE//DC(đpcm)
câu b bạn ghi thíu đề
Đúng 0
Bình luận (0)
câu b là cm: tam giác DAH = tam giác ABH
mik có đề y hệt
Đúng 0
Bình luận (0)
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân
Đọc tiếp
1) cho tam giác vuông ABC đường cao AH .gọi AD ;AE là phân giác các góc BAH và góc CAH .chứng minh rằng đường tròn nội tiếp tam giác BCA trùng với đường tròn ngoại tiếp tam giác ADE
2)cho tam giác ABC vuông tại A;gọi I là tâm đường tròn nội tiếp tam giác ABC ;các tiếp điểm trên BC;CA;AB lần lượt là D,E,F.gọi M là trung điểm của AC ,đường thẳng MI cắt các cạnh AB tại N ,đường thẳng DF cắt đường cao AH tại P .cmr tam giác APN cân
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD. Chứng minh rằng ∠(EAF) = 900.
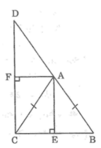
Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
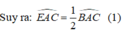
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
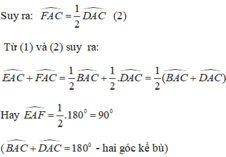
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A, đường cao AD, phân giác AE, Tính các góc của tam giác, biết BE = 2AD.
Cho tam giác ABC cân tại A . Đường cao AH . Kẻ HD vuông góc với AB , HE vuông góc với AC a, cm AD =AE b, cm tam giác BDH=tam giác CEH
a) trong tam giác cân đường cao đồng thời là đường phân giác nên AH cũng là đường phân giác nên góc BAH = góc CAH
Xét ΔADH và ΔAEH có:
góc ADH=góc AEH (= 90o)
chung AH
góc HAD = góc HAE (cmt)
⇒ΔADH = ΔAEH(ch-gn)
⇒ DH = EH (2 cạnh tương ứng)
b) trong tam giác cân đường cao đồng thời là đường trung tuyến nên AH cũng là đường trung tuyến nên HB = HC
Xét ΔBDH và ΔCEH có:
góc BDH = góc CEH (=90o)
HB=HC(cmt)
góc B = góc C (ΔABC cân tại A)
⇒ ΔBDH = ΔCEH(ch-gn)
Đúng 1
Bình luận (0)
Hình vẽ: Bạn tự vẽ hình nhé !
a, Ta có:
△ABC cân tại A nên ∠ABC= ∠ACB hay ∠ABH= ∠ACH
và AB= AC
Xét △AHB và △AHC, có:
AB= AC ( theo chứng minh trên )
∠ABH= ∠ACH ( theo chứng minh trên )
AH: cạnh chung
Nên: △AHB= △AHC ( c.g.c)
⇒ ∠BAH= ∠CAH ( 2 góc tương ứng ) hay ∠DAH= ∠EAD
Xét △ADH và △AEH, có:
∠HDA= ∠HEA=90o ( Do HD ⊥ AB, HE ⊥ AC )
AH: cạnh chung
∠DAH= ∠EAH ( theo chứng minh trên )
Nên: △ADH= △AEH ( cạnh huyền- góc nhọn )
⇒ AD= AE ( 2 cạnh tương ứng ) ( đcpcm )
b,
Ta có: Do △ADH= △AEH nên :HD= HE ( 2 cạnh tương ứng )
AB= AC
⇒ AD+ DB= AE+EC
mà AD= AE nên DB= EC
Xét △BDH và △CEH, có:
∠BDH= ∠CEH=90o
HD= HE ( theo chứng minh trên )
DB= EC ( theo chứng minh trên )
Nên △BDH= △CEH ( c.g.c ) ( đcpcm)
Đúng 0
Bình luận (2)
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{DAH}=\widehat{EAH}\)
Xét ΔDAH vuông tại D và ΔEAH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)(cmt)
Do đó: ΔDAH=ΔEAH(Cạnh huyền-góc nhọn)
Suy ra: AD=AE(Hai cạnh tương ứng)
b) Xét ΔDBH vuông tại D và ΔECH vuông tại E có
HB=HC(ΔABH=ΔACH)
HD=HE(ΔDAH=ΔEAH)
Do đó: ΔDBH=ΔECH(cạnh huyền-cạnh góc vuông)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H a, Chứng minh: AE=AD b,kẻ HK vuông góc với BC,K thuộc BC .Chứng minh AK là tia phân giác của góc BAC
Xem chi tiết
a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC
Đúng 2
Bình luận (0)





















