Trên mặt phẳng tọa độ Oxy xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA+OB=1 Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
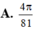
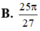
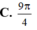
![]()
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
A. 4 π 81
B. 25 π 27
C. 9 π 4
D. 17 π 9
Đáp án A
Khi quay ∆ O A B quanh trục Oy, ta được hình nón có bán kính đáy r = OA và chiều cao h = OB. Theo bài ra, ta có OA + OB = r + h = 1 với (0 < r, h < 1)
Khi đó, thể tích khối nón là V N = 1 3 πr 2 h = 1 3 πr 2 1 - r .
Ta có r 2 1 - r 2 = 4 . r 2 . r 2 . 1 - r ≤ 4 . r 2 + r 2 + 1 - r 3 27 = 4 27 ⇒ V N ≤ 1 3 π . 4 27 = 4 π 81 .
Tham khảo: Ta có thể đưa điểm B có tung độ âm về tung độ dương thì thể tích của khối nón không đổi.
Gọi A a ; 0 B 0 ; b a , b > 0 suy ra phương trình đường thẳng A B : x y + y b = 1 ⇒ x = a - a b . y .
Khi đó V O y = π . ∫ a b a - a b y 2 d y = πa 2 b 3 .
Ta có 4 π 3 . a 2 . a 2 . b ≤ 4 π 3 . a 2 + a 2 + b 3 27 = 4 π 81 ⇒ V M a x = 4 π 81 .
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông AOB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác AOB quanh trục Oy bằng bao nhiêu?
A. 4 π 81
B. 15 π 27
C. 9 π 4
D. 17 π 9
Trong mặt phẳng Oxy cho tam giác đều OAB có cạnh bằng 2, AB song song với Ox, điểm A có hoành độ và tung độ dương
a) Tìm tọa độ hai đỉnh A và B
b) Tìm tọa độ trọng tâm G của tam giác OAB
a) Do AB//Ox và tam giác OAB đều nên điểm A đối xứng với điểm B qua Ox.
Suy ra: AB = 2 = 2b. Nên b = 1.
Áp dụng định lý Pi-ta-go: \(OH=\sqrt{AB^2-HA^2}=\sqrt{2^2-1^2}=\sqrt{3}\).
Suy ra: \(a=\sqrt{3}\Rightarrow x_A=\sqrt{3};y_B=-\sqrt{3}\).
Vậy \(A\left(1;\sqrt{3}\right),B\left(-1;-\sqrt{3}\right)\).
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A(2;1);điểm B nằm trên trục hoành,điểm C nằm trên trục tung sao cho các điểm B,C có tọa độ không âm.Tìm tọa độ các điểm B;C sao cho tam giác ABC có diện tích lớn nhất.
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp : E : x 2 4 + y 2 = 1 và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
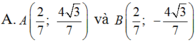
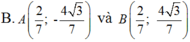
![]()
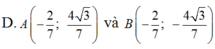
Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
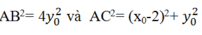
Vì A thuộc (E) nên:
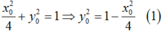
Vì AB = AC nên:
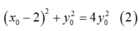
Thay (1) vào (2) ta được:
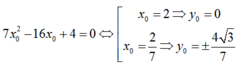
Vì điểm A khác C và Acó tung độ dương nên:
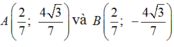
Trên mặt phẳng tọa độ Oxy có A(3;0);B(3;4).Biết tam giác ABC vuông cân tại B và C có hoành độ âm.Khi đó tọa độ của C là .....
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC vuông tại A(2;1), đường thẳng BC: 4x-3y+5=0. P là một điểm di động trên cạnh AC (P khác A và C). Đường tròn đường kính PC cắt BP tại I sao cho: BP.BI + CP.CA=25. Biết rằng B, C có tọa độ nguyên và C có hoành độ lớn hơn B. Hoành độ của điểm B là
A.-2
B. -1
C. 1
D. 2
Trong mặt phẳng Oxy. Các khẳng định sau đúng hay sai?
a) Tọa độ của điểm A bằng tọa độ của vectơ OA;
b) Điểm A nằm trên trục hoành thì có tung độ bằng 0;
c) Điểm A nằm trên trục tung thì có hoành độ bằng 0;
d) Hoành độ và tung độ của điểm A bằng nhau khi và chỉ khi A nằm trên tia phân giác của góc phần tư thứ nhất.
a) Đúng. Giả sử A(a; b); O(0; 0) 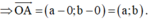
b) Đúng
c) Đúng
d) Đúng Vì tia phân giác của góc phần tư thứ nhất là đường thẳng y = x.
Trên mặt phẳng tọa độ Oxy có A(3;0); B(3;4). Biết tam giác ABC vuông cân tại B và C có hoành độ âm.
Khi đó tọa độ của C là